1 引 言

　　無線傳感器網絡作為一種全新的信息獲取和處理技術在目標跟蹤、入侵監測及一些定位相關領域有廣泛的應用前景。然而， 無論是在軍事偵察或地理環境監測， 還是交通路況監測或醫療衛生中對病人的跟蹤等應用場合， 很多獲取的監測信息需要附帶相應的位置信息， 否則， 這些數據就是不確切的，甚至有時候會失去采集的意義， 因此網絡中傳感器節點自身位置信息的獲取是大多數應用的基礎。首先， 傳感器節點必須明確自身位置才能詳細說明“在什么位置發什么了什么事件”， 從而實現對外部目標的定位和跟蹤； 其次， 了解傳感器節點的位置分布狀況可以對提高網絡的路由效率提供幫助， 從而實現網絡的負載均衡以及網絡拓撲的自動配置， 改善整個網絡的覆蓋質量。因此， 必須采取一定的機制或算法來實現無線傳感器網絡中各節點的定位。

　　無線傳感器網絡定位最簡單的方法是為每個節點裝載全球衛星定位系統（GPS） 接收器， 用以確定節點位置。但是， 由于經濟因素、節點能量制約和GPS 對于部署環境有一定要求等條件的限制， 導致方案的可行性較差。因此， 一般只有少量節點通過裝載GPS 或通過預先部署在特定位置的方式獲取自身坐標。另外， 無線傳感器網絡的節點定位涉及很多方面的內容， 包括定位精度、網絡規模、錨節點密度、網絡的容錯性和魯棒性以及功耗等， 如何平衡各種關系對于無線傳感器網絡的定位問題非常具有挑戰性。可以說無線傳感器網絡節點自身定位問題在很大程度上決定著其應用前景。因此， 研究節點定位問題不僅必要， 而且具有很重要的現實意義。

　　2 WSN 定位技術基本概念

　　2.1 定位方法的相關術語

　　1） 錨節點（anchors）： 也稱為信標節點、燈塔節點等， 可通過某種手段自主獲取自身位置的節點；

　　2） 普通節點（normal nodes）： 也稱為未知節點或待定位節點， 預先不知道自身位置， 需使用錨節點的位置信息并運用一定的算法得到估計位置的節點；

　　3） 鄰居節點（neighbor nodes）： 傳感器節點通信半徑以內的其他節點；

　　4） 跳數（hop count）： 兩節點間的跳段總數；

　　5） 跳段距離（hop distance）： 兩節點之間的每一跳距離之和；

　　6） 連通度（connectivity）： 一個節點擁有的鄰居節點的數目；

　　7） 基礎設施（infrastructure）： 協助節點定位且已知自身位置的固定設備， 如衛星基站、GPS 等。

　　2.2 定位方法的性能評價標準

　　無線傳感器網絡定位性能的評價標準主要分為7 種， 下面分別進行介紹。

　　1） 定位精度。定位技術首要的評價指標就是定位精確度， 其又分為絕對精度和相對精度。絕對精度是測量的坐標與真實坐標的偏差， 一般用長度計量單位表示。相對誤差一般用誤差值與節點無線射程的比例表示， 定位誤差越小定位精確度越高。

　　2） 規模。不同的定位系統或算法也許可以在一棟樓房、一層建筑物或僅僅是一個房間內實現定位。

　　另外， 給定一定數量的基礎設施或一段時間， 一種技術可以定位多少目標也是一個重要的評價指標。

　　3） 錨節點密度。錨節點定位通常依賴人工部署或使用GPS 實現。人工部署錨節點的方式不僅受網絡部署環境的限制， 還嚴重制約了網絡和應用的可擴展性。而使用GPS 定位， 錨節點的費用會比普通節點高兩個數量級， 這意味著即使僅有10%的節點是錨節點， 整個網絡的價格也將增加10 倍， 另外， 定位精度隨錨節點密度的增加而提高的范圍有限， 當到達一定程度后不會再提高。因此， 錨節點密度也是評價定位系統和算法性能的重要指標之一。

　　4） 節點密度。節點密度通常以網絡的平均連通度來表示， 許多定位算法的精度受節點密度的影響。

　　在無線傳感器網絡中， 節點密度增大不僅意味著網絡部署費用的增加， 而且會因為節點間的通信沖突問題帶來有限帶寬的阻塞。

　　5） 容錯性和自適應性。定位系統和算法都需要比較理想的無線通信環境和可靠的網絡節點設備。

　　而真實環境往往比較復雜， 且會出現節點失效或節點硬件受精度限制而造成距離或角度測量誤差過大等問題， 此時， 物理地維護或替換節點或使用其他高精度的測量手段常常是困難或不可行的。因此， 定位系統和算法必須有很強的容錯性和自適應性， 能夠通過自動調整或重構糾正錯誤， 對無線傳感器網絡進行故障管理， 減小各種誤差的影響。

　　6） 功耗。功耗是對無線傳感器網絡的設計和實現影響最大的因素之一。由于傳感器節點的電池能量有限， 因此在保證定位精確度的前提下， 與功耗密切相關的定位所需的計算量、通信開銷、存儲開銷、時間復雜性是一組關鍵性指標。

　　7） 代價。定位系統或算法的代價可從不同的方面來評價。時間代價包括一個系統的安裝時間、配置時間、定位所需時間； 空間代價包括一個定位系統或算法所需的基礎設施和網絡節點的數量、硬件尺寸等； 資金代價則包括實現一種定位系統或算法的基礎設施、節點設備的總費用。

　　上述7 個性能指標不僅是評價無線傳感器網絡自身定位系統和算法的標準， 也是其設計和實現的優化目標。為了實現這些目標的優化， 有大量的研究工作需要完成。同時， 這些性能指標相互關聯， 必須根據應用的具體需求做出權衡以設計合適的定位技術。

　　3 主要的WSN 定位方法

　　WSN 的定位方法較多， 可以根據數據采集和數據處理方式的不同來進行分類。在數據采集方式上， 不同的算法需要采集的信息有所側重， 如距離、角度、時間或周圍錨節點的信息， 其目的都是采集與定位相關的數據， 并使其成為定位計算的基礎。在信息處理方式上， 無論是自身處理還是上傳至其他處理器處理， 其目的都是將數據轉換為坐標， 完成定位功能。目前比較普遍的分類方法有3 種：

　　1） 依據距離測量與否可劃分為： 測距算法和非測距算法。其中測距法是對距離進行直接測量， 非測距法依靠網絡連通度實現定位， 測距法的精度一般高于非測距法， 但測距法對節點本身硬件要求較高，在某些特定場合， 如在一個規模較大且錨節點稀疏的網絡中， 待定位節點無法與足夠多的錨節點進行直接通信測距， 普通測距方法很難進行定位， 此時需要考慮用非測距的方式來估計節點之間的距離，兩種算法均有其自身的局限性；2） 依據節點連通度和拓撲分類可劃分為： 單跳算法和多跳算法。單跳算法較多跳算法來說更加的簡便易行， 但是存在著可測量范圍過小的問題， 多跳算法的應用更為廣泛， 當測量范圍較廣導致兩個節點無法直接通信的情況較多時， 需要多跳通信來解決；3） 依據信息處理的實現方式可劃分為： 分布式算法和集中式算法。以監測和控制為目的算法因為其數據要在數據中心匯總和處理， 大多使用集中式算法， 其精度較高， 但通信量較大。分布式算法是傳感器節點在采集周圍節點的信息后， 在其自身的后臺執行定位算法， 該方法可以降低網絡通信量， 但目前節點的能量、計算能力及存儲能力有限， 復雜的算法難以在實際平臺中實現。

　　普遍認為基于測距和非測距的算法分類更為清晰， 本文以其為分類原則介紹主要的WSN 定位方法。此外， 由于目前非測距算法大多為理論研究， 且實用性較差， 因此， 本文將著重介紹基于測距的定位方法。

　　3.1 基于測距的算法

　　基于測距的算法通常分為2個步驟， 首先利用某種測量方法測量距離（或角度）， 接著利用測得的距離（或角度）計算未知節點坐標。下面分別進行介紹。

　　3.1.1 距離的測量方法

　　本節將詳細說明3 種主流的測量方法， 第一種是基于時間的方法， 包括基于信號傳輸時間的方法（time of arrival， TOA）和基于信號傳輸時間差的方法（time difference of arrival， TDOA）； 第二種是基于信號角度的方法（angle of arrival， AOA）； 第三種是基于信號接收信號強度的方法（received signal strengthindicator， RSSI）方法。下面分別進行介紹。

　　1） 基于時間的方法

　　a. 基于信號傳輸時間的方法：

　　TOA 技術通過測量信號的傳播時間來計算距離，該技術可分為單程測距和雙程測距， 單程測距即信號只傳輸一次， 雙程測距即信號到達后立即發回。前者需要兩個通信節點之間具有嚴格的時間同步， 后者則不需要時間同步， 但是本地時鐘的誤差同樣會造成很大的距離偏差。最典型的應用就是GPS 定位系統。

　　優點： 測量方法簡單且能取得較高的定位精度。

　　缺點： Ⅰ。 精確計時難。通常傳感節點之間通信都采用無線電信號， 由于無線電的傳輸速度非常快，而傳感節點之間的距離又較小， 這使得計算發送節點和接收節點之間的信號傳輸時間非常困難。因此利用此技術定位的節點需要采用特殊硬件來產生用于發送和接收的慢速無線信號。Ⅱ。 高精度同步難。

　　有些算法還需要接收節點和發送節點之間具有嚴格的時間同步， 時間同步的問題現在也是無線傳感器網絡中的一個研究熱點并且沒有完全解決， 這也限制了算法的實用性。Ⅲ。 易受噪聲影響。在空間傳輸的信號會受到各種噪聲的影響， 所以即使在不同的測量中得到了相同的信號傳輸時間也不能斷定這兩次測量中的發送節點和接收節點間的距離是相同的。

　　最早的TOA 距離估計算法是在非時間同步網絡中利用對稱雙程測距協議進行測量的。之后， 單邊測距方法在后續的研究中被提出， 如Harter 開發的Active Bat 定位系統［10］， 它由一系列固定在網格中的節點組成。固定節點從移動節點中接收超聲波， 并通過TOA 算法計算到移動節點的距離， 在通信范圍30 m 左右的情況下， 其定位精度達到9 cm， 相對精度9.3%。但TOA 只有在視距（line-of-sight， LOS）的情況下才比較精確， 在非視距（none line-of-sight， NLOS）情況下， 隨著傳播距離的增加測量誤差也會相應增大。綜述了在視距和非視距情況下多種TOA 距離估計方法所需要的復雜度， 先驗知識和實驗結果等。Hangoo Kang 等人在多徑環境下利用基于啁啾展頻技術（chirp spread spectrum， CSS） 和對稱雙邊雙向測距技術（symmetric double sided two-wayranging， SDS-TWR） 的TOA 定位系統中提出了誤差補償算法， 取得了較好的定位效果， 在此基礎上Andreas Lewandowski 等人提出了一種加權的TOA 算法， 該算法應用于工業環境下， 可提高系統容錯性， 降低自身對測距系統的干擾， 在7 m×24.5 m 的范圍內， 測距誤差小于3 m。

　　b. 基于信號傳輸時間差的方法：

　　TDOA 測距技術廣泛應用于無線傳感器網絡的定位方案中。通常在節點上安裝超聲波收發器和射頻收發器， 測距時錨節點同時發送超聲波和電磁波，接收節點通過兩種信號到達時間差來計算兩點之間距離。

　　優點： 在LOS 情況下能取得較高的定位精度。

　　缺點： Ⅰ。 硬件需求較高。傳感節點上必須附加特殊的硬件聲波或超聲波收發器， 這會增加傳感節點的成本； Ⅱ。 傳輸信號易受環境影響。聲波或者超聲波在空氣中的傳輸特性和一般的無線電波不同，空氣的溫度、濕度或風速都會對聲波的傳輸速度產生較大的影響， 這就使得距離的估計可能出現一定的偏差， 使用超聲波與RF 到達時間差的測距范圍為5～7 m， 實用性不強， 且超聲波傳播方向單一， 不適合面向多點傳播； Ⅲ。 應用場合單一。測距的前提是發送節點和接收節點之間沒有障礙物阻隔， 在有障礙物的情況下會出現聲波的反射、折射和衍射， 此時得到的實際傳輸時間將變大， 在這種傳輸時間下估算出的距離也將出現較大的誤差。

　　由MIT 開發出的Cricket 室內定位系統最早采用了RF 信號與超聲波信號組合的TDOA測距技術， 在2 m×2 m×2.5 m 的范圍內， 該系統定位精度在10 cm以下， 現已成為Crossbow 的商業化產品。加利福尼亞大學洛杉磯分校的Medusa 節點在AHLos定位系統之間傳輸距離為3 m 左右時， 測距精度能夠達到厘米級別。加州大學伯克利分校開發的Calamari定位系統均采用TDOA 超聲波測距， 在144 m2 的區域部署49 個節點， 平均定位誤差達到0.78 m， 文獻對于聲波收發器的方向單一性問題， 給出了兩種解決方法： 一是將多個傳感器調整成向外發射的形狀； 二是在節點的平面上使用金屬圓錐來均勻地傳播和收集聲波能量。結合TDOA 測距機制和NTP 協議時間同步原理， 一些學者提出了時間同步與節點測距混合算法， 結合基于到達時間差的測距機制和網絡時間協議中的時鐘同步機制， 通過逆推時間非同步情況下相互測距的意義， 不僅能實現時間同步， 還可以實現相對測距甚至絕對測距。

　　基于時間的定位方法的定位精度雖高， 但從上面的例子中可以看出其測距距離較短， 且附加的硬件將增加節點的體積和功耗， 不適于實際應用。

　　2） 基于信號到達角度的方法

　　AOA 測距技術依靠在節點上安裝天線陣列來獲得角度信息。由于大部分節點的天線都是全向的， 無法區分信號來自于哪個方向。因此該技術需要特殊的硬件設備如天線陣列或有向天線等來支持。

　　優點： 能夠取得不錯的精度。

　　缺點： 傳感節點最耗能的部分就是通信模塊，所以裝有天線陣列的節點的耗能、尺寸以及價格都要超過普通的傳感節點， 與無線傳感器網絡低成本和低能耗的特性相違背， 所以實用性較差。

　　關于AOA 定位的文獻比較少，最早提出在室內采集方向信息， 并以此實現定位的方法，它的硬件部分包括微控制器、RF 接收器、5 個排成“V”型的超聲波接收器， 其測量誤差精度為5°。隨后， 一些學者提出了在只有部分節點有定位能力的情況下確定所有節點的方向和位置信息的算法。

　　3） 基于接收信號強度的方法

　　RSSI 是在已知發射功率的前提下， 接收節點測量接收功率， 計算傳播損耗， 并使用信號傳播模型將損耗轉化為距離。

　　優點： 低成本。每個無線傳感節點都具有通信模塊， 獲取RSSI 值十分容易， 無需額外硬件。

　　缺點： 1） 錨節點數量需求多。由于RSSI 值在實際應用中的規律性較差， 使得利用RSSI 信息進行定位的算法在定位精度以及實用性上存在缺陷。所以為了達到較高的定位精度， 利用RSSI 信息進行定位的算法通常需要較多數量的錨節點。2） 多路徑反射、非視線問題等因素都會影響距離測量的精度。

　　早期的RSSI 距離測量方法有Hightower 等人設計的室內定位SpotON tags 系統， 通過RSSI 方法來估計兩點間的距離， 通過節點間的相互位置來進行定位， 在邊長3 m 的立方體內， 其定位精度在1 m 以內。目前， 基于RSSI 值的距離測量方法可以分為2 種， 一種是需要預先測試環境信息的方法， 即在實驗開始前， 對定位的區域進行大量的RSSI 值測試，將不同點得到的RSSI 值保存到數據庫中， 建成場強圖或擬合曲線， 在實際測試時查詢和調用。另外一種是無需預先測試環境信息的方法， 直接在定位區域進行節點布置和定位， 如雙曲線模型法，迭代的分布式算法， 結合露珠洪泛思想引入RSSI 機制的HCRL（hop-count-ratio based localization）算法等。

　　總體來說， 需要預先測試環境參數的方法在實際定位中計算量小， 這類方法只需要簡單的查表或根據擬合曲線進行計算， 其缺點是實驗前需要做大量的準備工作， 而且一旦環境改變則預先建立的模型將不再適用。無需預先測試環境參數的方法需要定位引擎的計算操作， 往往具有復雜的計算過程，但適應性較強。

　　以上幾種測距方法各有利弊， 以2009 年發表的基于測距法的文獻來看， 研究RSSI 方法的大約占了以上幾種方法總數的52%， TOA 方法25%， TDOA 方法13%和AOA 方法10%， 其比例圖如圖1 所示， 從實用性的角度來看， 基于RSSI 的定位方法更簡便易行， 因此， 基于RSSI 測距方法的研究占基于測距算法研究總數的一半以上。

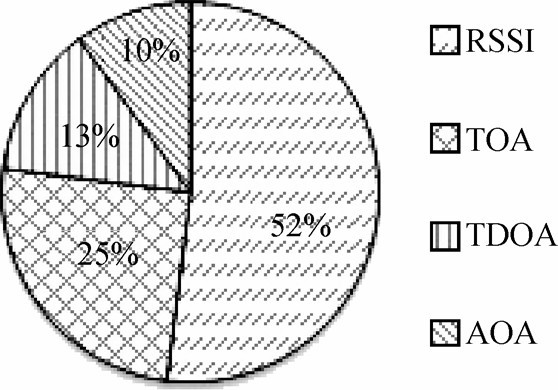
　　圖1 各類方法研究比例圖 

　　3.1.2 節點坐標計算方法

　　無線傳感器節點定位過程中， 當未知節點獲得與鄰近參考節點之間的距離或相對角度信息后， 通常使用以下原理計算自己的位置。

　　1） 三邊測量法是一種基于幾何計算的定位方法，如圖2 所示， 已知3 個節點A， B， C 的坐標以及3 點到未知節點的距離就可以估算出該未知點D 的坐標，同理也可以將這個結果推廣到三維的情況。

　　2） 三角測量法也是一種基于幾何計算的定位方法， 如圖3 所示， 已知3 個節點A， B， C 的坐標和未知節點D 與已知節點A， B， C 的角度， 每次計算2 個錨節點和未知節點組成的圓的圓心位置如已知點A， C與D的圓心位置O， 由此能夠確定3 個圓心的坐標和半徑。最后利用三邊測量法， 根據求得的圓心坐標就能求出未知節點D 的位置。

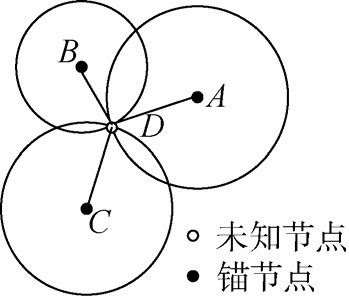
　　圖2 三邊測量法原理示意圖

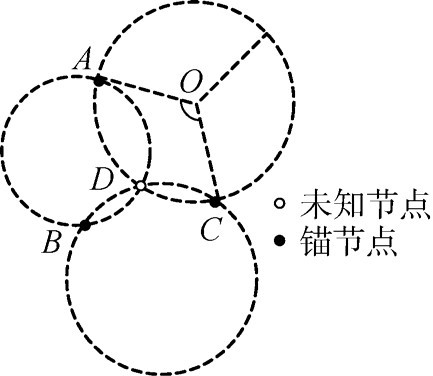
　　圖3 三角測量法原理示意圖

　　3） 極大似然估計法。如圖4 所示， 已知n 個點的坐標和它們到未知節點的距離， 列出坐標與距離的n 個方程式， 從第1 個方程開始， 每個方程均減去最后一個方程， 得到n？1 個方程組成的線性方程組，最后用最小二乘估計法可以得到未知節點的坐標。

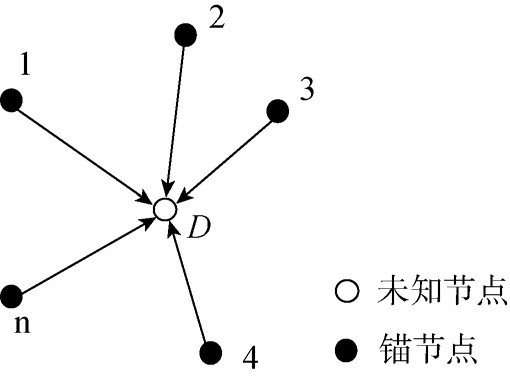
　　圖4 極大似然估計法原理示意圖

　　4） 極小極大定位算法， 在無線傳感器網絡定位中也被廣泛使用。如圖5 所示， 計算未知節點與錨節點的距離， 接著錨節點根據與未知節點的距離d， 以自身為中心， 畫以2d 為邊長的正方形， 所有錨節點做出的正方形中重疊的部分的質心就是未知節點的坐標。針對極小極大定位算法對錨節點密度依賴過高的問題， 有學者利用錨節點位置信息提出了分步求精定位算法， 該算法在只利用適量的錨節點的情況下可達到較高定位精度。

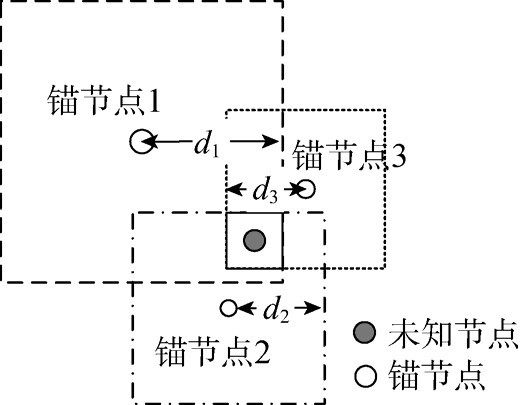
　　圖5 極小極大定位算法原理示意圖

 　　文獻［35］在12 m×19.5 m 的范圍內對上述三邊測量法、極大似然估計法和極小極大法方法的計算量和精度進行了測試。實驗表明， 極大似然估計法的計算量最大， 錨節點小于10 個時， 極小極大法的計算量最小， 在錨節點較少情況下， 三邊法和極小極大法的精確度較高， 而當錨節點超過6 個時， 極大似然估計法精確度更高。因此， 在計算坐標時要根據實際情況合理選擇坐標計算方法。另外， 針對現存的定位算法都是假設信標節點不存在誤差， 與真實情況不符的情況， 文獻［36］提出信標優化選擇定位算法（OBS）， 即通過減小定位過程中的誤差傳遞來提高定位精度。

　　3.2 基于非測距的算法

　　基于非測距的算法與測距法的區別在于前者不直接對距離進行測量， 而是使用網絡的連通度來估計節點距錨節點的距離或坐標， 由于方法的不確定性， 基于非測距的方法眾多。下面按時間順序，介紹部分典型非測距定位算法。

　　Bulusu 等人提出了一個單跳， 低功耗的算法，它利用錨節點的連通性來確定坐標。未知節點的坐標通過計算無線電范圍內所有節點的質心獲得。節點將自己定位在與它們表現相近節點的質心處， 該算法雖然簡單， 但誤差較大， 需要的錨節點密度較高。約90%節點的定位精度在錨節點分布間距的1/3以內。

　　He 等人提出了APIT 算法， 目標節點任選3 個相鄰錨節點， 測試未知節點是否位于它們所組成的三角形中。使用不同錨節點組合重復測試直到窮盡所有組合或達到所需定位精度。最后計算包含目標節點的所有三角形的交集質心， 并以這一點作為目標節點位置， 該算法需要較高的錨節點密度， 其定位精度為40%。

　　Niculescu 等人提出了DV-Hop 定位算法， 它從網絡中收集相鄰節點信息， 計算不相鄰節點之間最短路徑。DV-Hop 算法使用已知位置節點的坐標來估測一個跳躍距離， 并使用最短路徑的跳躍距離估計未知節點和錨節點的距離， 該算法僅適用于各向同性的密集網絡， 當錨節點密度為10%時， 定位誤差為33%。

　　Radhika 等人提出的Amorphous Positioning 算法，使用離線的跳躍距離估測， 同DV-Hop 算法一樣， 通過一個相鄰節點的信息交換來提高定位的估測值，需要預知網絡連通度， 當網絡連通度為15 時， 定位精度20%。

　　Savvides 等人介紹了一種N-Hop multilateration算法， 使用卡爾曼濾波技術循環求精， 該算法避免了傳感器網絡中多跳傳輸引起的誤差積累并提高了精度， 節點通信距離為15 m， 當錨節點密度為20%，測距誤差為1 cm 時， 定位誤差為3 cm。

　　Capkun 等人提出了self-positioning algorithm（SPA）， 該算法首先根據通信范圍在各個節點建立局部坐標系， 通過節點間的信息交換與協調， 建立全局坐標系統， 網絡中的節點可以在與它相隔N 跳的節點建立的坐標系中計算自己的位置。

　　綜上可知， 非測距算法多為理論研究， 其定位精度普遍較低并且與網絡的連通度及節點的密集程度密切相關， 因此， 其適用范圍有一定的局限性， 在進行無線傳感器網絡定位技術研究過程中應更多地考慮基于測距的定位算法。

　　4 新型WSN 定位研究分析

　　除了傳統的定位方法， 新型的無線傳感器網絡定位算法也逐漸出現， 如利用移動錨節點來定位未知節點、在三維空間內定位未知節點、以及采用智能定位算法來提高定位精度等， 下面分別介紹。

　　4.1 基于移動錨節點的定位算法

　　利用移動錨節點定位可以避免網絡中多跳和遠距離傳輸產生的定位誤差累計， 并且可以減少錨節點的數量， 進而降低網絡的成本。如MBAL（mobilebeacon assisted localization scheme）定位方法， 錨節點在移動過程中隨時更新自身的坐標， 并廣播位置信息。未知節點測量與移動節點處于不同位置時的距離， 當得到3 個或3 個以上的位置信息時， 就可以利用三邊測量法確定自己的位置， 進而升級為錨節點。此外， 移動錨節點用于定位所有未知節點所移動的路徑越長則功耗越大， 因此對移動錨節點的活動路徑進行合理規劃可以減小功耗。

　　文獻［48］提出了一種基于加權最小二乘法的移動錨節點定位距離估計算法， 作者首先建立一個移動模型， 錨節點沿著線性軌跡移動， 使用加權最小二乘法來減小距離估計誤差， 并在Cramér-Raobound（CRB） 的基礎上分析了距離估計的最小誤差邊界， 該算法在距離估計和位置估計方面都有較好的性能。

　　利用移動錨節點自身的可定位性和可移動性可定位網絡局部相關節點， 但移動錨節點的路徑規劃算法和采取的定位機制需要深入考慮。2009 年發表的關于WSN 定位的文章中， 約25%是關于移動節點定位的。

　　4.2 三維定位方法

　　隨著傳感器網絡的空間定位需求不斷提升， 三維空間場景下的定位也成為了一個新的研究方向。

　　目前的三維定位算法包括基于劃分空間為球殼并取球殼交集定位的思想， 提出的對傳感器節點進行三維定位的非距離定位算法APIS（approximatepoint in sphere） 。在此基礎上針對目前三維定位算法的不足， 提出的基于球面坐標的動態定位機制， 該機制將定位問題抽象為多元線性方程組求解問題，最終利用克萊姆法則解決多解、無解問題。建立了WSN 空間定位模型并結合無線信道對數距離路徑衰減模型， 為解決不適定型問題提出了Tikhonov 正則化方法， 并結合偏差遠離方便的得到了較優的正則化參數， 在3.5 m×6 m×3 m 的區域內定位精度可控制在2 m。

　　三維定位方法可擴展WSN 的應用場合， 目前三維定位在許多方面還有待完善， 如獲取更準確的錨節點需要尋求更精確的廣播周期和消息生存周期， 縮減定位時間需要改進錨節點的選擇和過濾機制等。

　　4.3 智能定位算法

　　隨著電子技術的發展和芯片計算能力的提高，傳感器網絡節點本身的性能也有提升， 復雜算法也可以在網絡中實現。因此， 智能定位算法也紛紛被提出。

　　對于無線傳感器網絡的戶外三維定位， 將錨節點固定在直升機上通過GPS 實時感知自身位置， 采用基于RSSI 的測距方法， 利用粒子濾波定位技術實現定位， 該方法不需要任何關于未知節點的先驗知識， 非常適合應用于戶外定位。

　　神經網絡對于解決無線傳感器網絡的定位問題是一個切實可行的辦法， 將3 種神經網絡： 多層感知神經網絡， 徑向基函數神經網絡和遞歸神經網絡與卡爾曼濾波的2 個變形進行比較， 可以根據不同情況下的定位需求靈活選擇定位方法。使用神經網絡和網格傳感器訓練的靈活的模型， 可以提高定位精度， 且不需要額外的硬件支持。網絡訓練每隔一段時間進行一次更新來最小化誤差， 并且通過增加網格節點密度來提高定位精度。

　　對于節點定位中的非視距問題， 常規的辦法是采用機器學習中的支持向量回歸（support vector regression，SVR） 方法進行定位以降低誤差， 但其定位精度仍然受到一定的非視距誤差影響， 為了降低這種影響， 研究人員提出了基于直推式回歸的定位算法。利用錨節點的坐標和TOA 信息并借用核函數直接推導出未知節點的位置， 進一步提高定位 精度。

　　雖然智能定位算法已經成為一個新的研究方向，但由于WSN 網絡本身屬于低能耗的網絡， 單個節點的計算能力還比較低， 目前智能定位算法不普遍適用于實際的WSN 定位系統， 但隨著低功耗技術、微處理器技術、FPGA 技術的發展， 智能定位算法將在未來的定位系統中得到廣泛的應用。

　　5 研究前景與應用分析

　　截至目前， 無線傳感器網絡定位研究已廣泛開展并取得了許多研究成果， 但仍存在著一些沒有被解決或被發現的問題， 目前最為關鍵的問題仍然是WSN 節點的能耗問題， 一切的定位算法應該在精度和能量消耗上選取一個較為折衷的效果。下面將對目前存在的問題及相應可能的解決方案進行介紹。

　　1） 實用性差。大部分基于非測距的定位算法只是停留在理論研究階段， 且大都是在仿真環境下進行的， 需要假設很多不確定因素， 而這些因素在實際應用中往往不能滿足， 則這些算法就失去了實際的意義。因此定位算法的設計應該更多的從實際應用上考慮， 結合實際應用情況設計實用的定位算法。

　　2） 應用環境單一。多數的算法都是針對特定的應用場景進行設計的， 也就是說， 每個算法都只能解決特殊的問題或應用于特定的場景， 一旦環境發生變動， 算法或系統的測量誤差將增大甚至不再適用。因此， 探索更具通用性的定位算法或定位系統， 將其應用于更為復雜多變的環境中是一項新的挑戰。

　　3） 受硬件限制。在實際定位中， 一些算法由于受到傳感器節點硬件成本和性能的限制， 如某些算法需要在定位節點上增加GPS， 超聲波收發器， 有向天線陣列等設備， 增加了節點硬件成本， 阻礙了其在實際定位系統中的應用。因此， 算法設計應多考慮WSN 節點的實際情況， 如只在部分節點上增加額外硬件， 或根據實際節點資源受限情況采用其他定位算法等。

　　4） 能量受限。測量精度、容錯性和能量消耗等問題也是目前無線傳感器網絡研究的熱點， 更是定位技術研究的熱點。通常情況下， 高測量精度和低能量消耗不可兼得， 往往需要在測量精度和能量消耗上進行有效的折衷。因此， 可以在提高儲能設備的容量， 或利用可能的外界環境資源為節點提供能量方向進行研究， 另外， 提出高效、節能、符合實際情況的無線傳感器網絡定位算法將具有現實的意義。

　　5） 安全和隱私問題。在大范圍部署的無線傳感器網絡中， 安全和隱私的問題也是一個主要的研究方向。一方面， 一些應用需要節點位置信息， 另一方面， 向一些不需要知道位置的節點透露位置信息則會使網絡面臨安全問題。此外， 鑒于無線傳感器網絡的性質， 集中式算法在后臺處理定位程序也使得節點的位置信息通過層層傳遞被過多的節點所知曉，因此分布式算法相對于集中式算法可以減少信息傳遞次數， 增強網絡安全性， 另外， 在網絡通信中使用信息加密也可以提高網絡安全性。就2009 年發表的定位相關文章來說， 每4 篇發表的文章中就有1 篇提出的是分布式算法。

　　未來的無線傳感器網絡定位在解決上述問題之后將廣泛應用于各類領域， 包括安全定位、變化的環境、三維空間等。

　　6 結 論

　　結合近年來無線傳感器網絡定位技術的發展狀況， 對無線傳感器網絡定位的基本概念、評價標準以及國內外研究現狀進行了概述， 重點對基于測距和基于非測距的無線傳感器網絡定位算法進行了分析， 并列舉了一些新型WSN 定位的算法， 總結了目前無線傳感器網絡定位領域研究存在的問題和一些可以研究的內容和方向。希望本文能夠為無線傳感器網絡定位相關領域的研究者提供一些參考和借鑒。