在用統計分析方法研究這個多變量的課題時,變量個數太多就會增加課題的復雜性。人們自然希望變量個數較少而得到的信息較多。在很多情形,變量之間是有一定的相關關系的,當兩個變量之間有一定相關關系時,可以解釋為這兩個變量反映此課題的信息有一定的重疊。主成分分析是對于原先提出的所有變量,建立盡可能少的新變量,使得這些新變量是兩兩不相關的,而且這些新變量在反映課題的信息方面盡可能保持原有的信息。
主成分分析(Principal Component Analysis,PCA), 將多個變量通過線性變換以選出較少個數重要變量的一種多元統計分析方法。又稱主分量分析。在實際課題中,為了全面分析問題,往往提出很多與此有關的變量(或因素),因為每個變量都在不同程度上反映這個課題的某些信息。主成分分析首先是由K.皮爾森對非隨機變量引入的,爾后H.霍特林將此方法推廣到隨機向量的情形。信息的大小通常用離差平方和或方差來衡量。
人們到醫院就診時,通常要化驗指標來協助醫生的診斷。診斷就診人員是否患腎炎時通常要化驗人體內各種元素含量,主要包括鋅(Zn)、銅(Cu)、鐵(Fe)、鈣(Ca)、鎂(Mg)、鉀(K)及鈉(Na)。表1是確診病例的化驗結果,其中1~30號病例是已經確診為腎炎病人的化驗結果,31~60號病例是已經確定為健康人的結果[2]。在論文中列出的數據是原始數據中1~10號病例及31~40號病例的數據,運用主成分計算時以所有數據為初始數據。

1 主成分分析模型
主成分分析是設法將原來眾多具有一定相關性(比如P個指標),重新組合成一組新的互相無關的綜合指標來代替原來的指標。通常數學上的處理就是將原來P個指標作線性組合,作為新的綜合指標。最經典的做法就是用F1(選取的第一個線性組合,即第一個綜合指標)的方差來表達,即Var(F1)越大,表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的,故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息,再考慮選取F2即選第二個線性組合,為了有效地反映原來信息,F1已有的信息就不需要再出現在F2中,用數學語言表達就是要求Cov(F1, F2)=0,則稱F2為第二主成分,依此類推可以構造出第三、第四,……,第P個主成分。

2 模型應用
2.1 問題分析解決

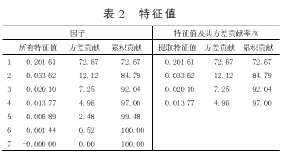
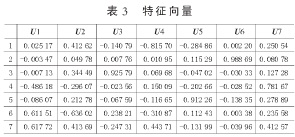
因C1=[X1 X2 … X7]*[U11 U12 … U17]T,因為特征值的方差貢獻率為72.67 %,表明C1包含原變量中的絕大部分信息,則在原來7個因子的基礎上引入C1作為第8個因子,C1=[0.70502、0.6341、0.87415、0.80724、0.4212、0.62897、0.37992、0.85489、0.57495、0.71527、-0.74635、0.03003、-0.30047、-0.03826、-0.80605、-1.32826、-0.5588、-0.00363、0.37216、-3.19199].再將其做標準化變化,再次通過主成分分析并結合SPSS軟件確定B第一主成分F1、第二主成分F2和綜合主成分F.根據對這8個因子通過SPSS的因子分析如表4、表5所示。

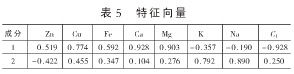
由表5可知C1與5種元素有著顯著的相關性,可見許多變量之間直接的相關性比較強,證明它們存在信息上的重疊。
2.2 主成分表達式
主成分個數提取原則為主成分對應特征值>1的前m個主成分。特征值在某種程度上可以被看成是表示主成分影響力度大小的指標,如果特征值<1,說明該主成分的解釋力度還不如直接引入原變量的平均解釋力度,因此一般可以用特征值>1作為納入標準。通過表4可知,提取2個主成分,即m=2.從表5可知C1、Zn、Cu、Fe、Ca、Mg在B第一主成分上有較高的載荷,說明B第一主成分基本反映了這些指標的信息,K、Na在B第二主成分上有較高的載荷,說明B第二主成分基本反映了K、Na 2個指標的信息。所以提取2個主成分是基本反映全部指標的信息,所以決定用2個新的變量來代替原來的8個變量。通過SPSS將表5中的數據除以主成分相對應的特征值開平方根,得到兩主成分中每個指標所對應的系數。將得到的特征向量與標準化后的數據相乘,然后就可以得到主成分表達式:
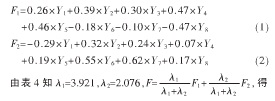
![]()
由(1)、(2)、(3)式得到B第一主成分F1、B第二主成分F2和綜合主成分F的數據及排名,如表6所示。
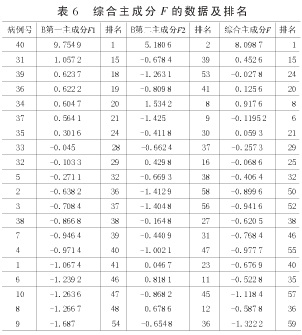
由表6可以看出第一主成分中以0為臨界值,0.1為修正值,即(-0.1,0.1)為不穩定狀態,此狀態下的就診人員將隨機被確定為患者和健康者中的1個。而當F1>0.1時,將此時對應的就診人員確定為健康者;當F1<-0.1時,將此時的就診人員確定為患者。經此方法判定的患者與健康者與表1中的患者與健康者基本一致,并且與用綜合主成分分析得到的結果基本一致。其判定的準確性可以達到95%以上,因此具備很強的可信性與科學性。
本文創新點在于模型中連續做了2次主成分分析,即二次主成分分析,并伴有大量的數據處理和數據分析,合理的結論背后擁有強大的理論支持和數據支持,具有很強的科學性和可信性。不過,確診病人還是需要通過醫生的具體分析,以達到所需效果。

