摘  要： 在最大頻繁項集的挖掘過程中，尤其在數據規模龐大并且最小支持度較小的情況下，超集檢測成為算法運行的主要時間消耗，提出最大頻繁項集算法A-MFI，其通過優化基于投影的超集檢測機制有效地減少了超集檢測的時間。另外，將事務數據庫數據映射至一種壓縮的AFOPT-tree結構，該結構結合自頂向下的遍歷策略，具有更小的時間開銷。

　　關鍵詞： 最大頻繁項集；關聯規則；超集檢測；最大頻繁項集投影

　　1993年AGRAWAL R等人提出了一個重要的反映大規模數據中項目集之間有趣的關聯或相關聯系的研究課題[1]，找出屬性間有價值的關系，即關聯規則的研究。頻繁項集的挖掘是獲取關聯規則不可或缺的步驟。但挖掘頻繁項集時需要考慮太多的候選項集。最大頻繁項集中已經隱含了所有的頻繁項集，并且在許多數據挖掘應用中也只需要挖掘最大頻繁項集，而不是獲取所有的頻繁項集，因此對最大頻繁項集的挖掘具有重大的現實意義。

　　已有的最大頻繁項集挖掘算法可以按照對搜索空間樹的遍歷策略分為寬度優先算法和深度優先算法兩種。其中，MaxMiner、DMFI和DMFIA為寬度優先算法。MaxMiner[2]采用傳統的橫向數據集來計算頻繁項集的支持度，雖然動態排序的方法能保證高效的前瞻剪枝，但掃描次數與Apriori[3]算法相同，掃描數據集的次數等于最長頻繁項集的規模。GenMax、SmartMiner、Fp-Max和FPMFI是挖掘最大頻繁項集的深度挖掘算法。算法GenMax[4]使用差集的方式表示事務數據庫，在稀疏事務數據庫的情況下有效減少了內存開銷，并提出使用局部最大頻繁項集的方式進行超集檢測。SmartMiner[5]算法使用尾信息進行數據挖掘，不需要超集檢測，但尾信息數據結構建立和訪問代價太高。Fp-Max[6]算法也是基于Fp-tree的最大頻繁項集挖掘算法，并將最大頻繁項集保存在MFI-tree[7]中，在一定程度上提高了挖掘效率。

　　本文提出的A-MFI（Ascending Frequency Ordered Prefix-tree For Maximal Frequent Item Set）算法通過對基于投影超集檢測方法[8]的優化，有效地提升了超集檢測的效率；并采用AFOPT-tree（Ascending Frequency Ordered Prefix-tree）[9]來存儲數據挖掘的相關信息，有效地減少了自頂向下遍歷的時間開銷和遞歸次數[10]。

　　1 相關知識

　　1.1 頻繁項集和最大頻繁項集

　　設I={i1，i2，i3，…，in}是一個項目集合，給定事務數據庫D，對于項目集X?哿I且k=|X|，稱X為k項集，或者簡稱為一個項集。記D為事務T的集合且T?哿I。對于給定的事務數據庫D，定義X的支持度為D中包含X的事務個數，記為Sup（X）。用戶自定義一個小于|D|的最小支持度，記為min_s。

　　定義1 給定書屋數據庫D和最小支持度min_s，對于項集X?哿I，若Sup（X）≥min_s，則稱X為D中的頻繁項集。

　　定義2 給定事務數據庫D和最小支持度min_s，對于項集X?哿I，若Sup（X）≥min_s并且對于任意（Y?哿I∧X?哿Y）均有Sup（Y）≦min_s，則稱X為D的最大頻繁項集。

　　性質1 任何頻繁項集的真子集都不是最大頻繁項集。

　　1.2 頻繁模式樹AFOPT-tree

　　Liu Guimei等提出使用一種稱為AFOPT-tree[9]的數據結構來存儲數據庫中與當前挖掘過程相關的頻繁信息。AFOPT-tree中每個結點對應一個項。樹中每一條從根結點到某個子孫結點的路徑表示一個項集，每個結點記錄了根結點到該結點的路徑對應項集的支持度。由于某些項集前部項的重疊，AFOPT-tree可以通過共享這些重疊的項來達到壓縮保存的目的。

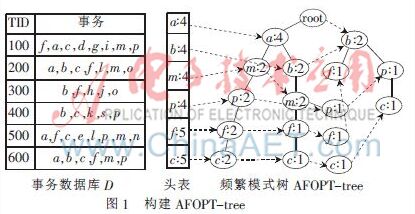
　　AFOPT-tree中有頭表，頭表中的頻繁1-項集按照頻繁次數的升序排列，它記錄了相應頻繁項的名稱和支持度。AFOPT-tree樹體中相同項的指針鏈接在一條鏈表上，鏈首指針也保存在頭表中。數據庫中的各項事務項集也按照頭表中的次序添加到頻繁模式樹中。給定一個事務數據庫D，與其對應的AFOPT-tree如圖1所示。AFOPT-tree的建立需要掃描兩次數據庫，AFOPT子樹的建立需要掃描兩次搜索空間中結點的AFOPT子樹中相應的條件模式基[10]。

　　2 基于AFOPT-tree的最大頻繁項集挖掘算法A-MFI

　　2.1 優化的基于投影的超集檢測

　　AFOPT-tree的頭表和加入的事務項集都是按照頻繁次數的升序排列的，按照頭表中頻繁1-項集的順序挖掘出的頻繁項集若存在超集，則必定在已挖掘到的最大頻繁項集中[11]。

　　MFI即最大頻繁集，是所有的最大頻繁項目集組成的集合。MFI-tree是類似于AFOPT-tree的樹形結構，用來存儲最大頻繁項集。從根節點到葉子節點的一條路徑就是最大頻繁項，中間節點不記錄支持度，只有葉子節點記錄支持度數。這里將MFI-tree樹體中相同項的指針鏈接在一條鏈表上，鏈首指針也保存在頭表中[12]。

　　在進行超集檢測時，不需要對整棵MFI-tree進行投影，先檢測待檢測項集的第一項在頭表中指向MFI-tree的指針是否為空。若為空，則不需要投影，直接添加到MFI-tree中；若不為空，將待檢測項集第一項為根節點構建MFI子樹。MFI子樹構建過程只需要掃描一次MFI-tree中對應結點的后繼結點。

　　對于圖1中的AFOPT-tree中已挖掘的最大頻繁項集{ampfc：3}，MFI-tree如圖2所示。有項集{bc：3}，檢查其是否在MFI-tree中存在超集。首先檢測頻繁1-項集b指向MFI-tree的指針為空，故項集在MFI-tree中不存在超集，將項集作為最大頻繁項集加入到MFI-tree中，如圖2所示虛線分支。再檢測項集{bf：3}，因為頻繁1-項集b指向MFI-tree的指針不為空，構建以b為根節點的MFI子樹，采用基于投影的超集檢測該項集在其中不存在超集，將項集作為最大頻繁項集加入到MFI-tree中，如圖2所示加粗分支。

　　2.2 A-MFI算法

　　與FP-max算法一樣，A-MFI算法采用分治遞歸的策略進行挖掘。在深度優先遍歷搜索AFOPT-tree時，通過對遍歷到的節點及對應的AFOPT子樹頭表中的某一項來生成搜索空間的子節點。并在構建AFOPT子樹之前先通過優化的基于投影的超集檢測來檢測首尾項集的并集在已有的最大頻繁項集是否存在超集。若存在，則可以進行前瞻剪枝；若不存在，遞歸的調用算法直到挖掘到某個子孫節點的AFOPT子樹為一個單路徑樹為止，將這個單路徑樹頭表中項集和對應前綴節點的并集作為一個最大頻繁項集，加入到MFI-tree中。

　　2.3 算法步驟

　　全局變量：前綴項集p，最大頻繁項集樹MFI-tree

　　輸入：數據量對應的AFOPT-tree，記為T，AFOPT-tree頭表中對應的項集h

　　輸出：最大頻繁項集樹MFI-tree

　　A-MFI（T，h）

　　（1）if T是單路徑樹。

　　（2）將項集p∪h插入MFI-tree中，支持度為單路徑樹中葉子節點的支持度。

　　（3）else對T頭表中的每一項i。

　　（4）將i并入前綴項集p中，為p′。

　　（5）遍歷AFOPT-tree獲取p′對應的子樹頭表項集h′。

　　（6）對p′∪h′進行超集檢測。

　　（7）if在MFI-tree中不存在超集。

　　（8）創建AFOPT子樹T′。

　　（9）A-MFI（T′，h′）。

　　（10）將i從p中移除。

　　3 實驗分析

　　為驗證算法性能，在內存為DDR3 2 GB、CPU為Core i5-2410M、操作系統為Windows 7 Professional的實驗環境下，用VC++ 6.0分別實現了A-MFI算法、FP-max算法和FPMFI算法。實驗采用的數據為參考文獻[12]中的Mushroom數據庫。該數據庫中共有8 124條事務記錄，平均事務長度為23，一共包含了蘑菇的115種屬性。A-MFI與FP-max和FPMFI的運行時間比較如圖3所示。

　　從圖3的實驗結果可以看出，由于A-MFI算法對基于投影的超集檢測機制進行了優化，并在存儲與數據挖掘相關數據時應用了AFOPT-tree樹形結構，在支持度較小時，尤其當支持度小于1%時，相比FPMFI算法和FP-max算法在執行時間上有較大優勢。例如在最小支持度為0.1%時，算法FP-max、FPMFI和A-MFI的執行時間分別為15.9 s，8.7 s和6.4 s，算法A-MFI的性能比較同類算法有明顯的提升。

　　本文提出了一種基于AFOPT-tree的最大頻繁項集挖掘算法，通過對基于投影的超集檢測機制進行優化，降低了超集檢測的時間消耗；采用AFOPT-tree樹形結構存儲與數據挖掘相關的信息，提升自頂向下的遍歷效率并減少遞歸次數。實驗比較表明，在支持度較小的情況下，本文的A-MFI算法具有明顯的優越性。在算法的執行過程中，遞歸構建AFOPT子樹和超集檢測消耗了大量的時間和內存，如何進一步地減少遞歸次數并提高超集檢測的效率是以后研究的重點。

　　參考文獻

　　[1] AGRAWAL R， IMIELINSKI T， SWAMI A. Mining association rules between sets of items in large databases[C]. Proceedings of ACM SIGMOD International Conference on Management of Data，1993：207-216．

　　[2] BAYARDO R. Efficiently mining long patterns from databases[C]. Proceeding of 1998 ACM S1 GMOD International Conference on Management of Data， New York： ACM Press， 1998：85-93．

　　[3] AGRAWAL R， SRIKANT R. Fast algorithms for mining association， rules[C]. Proceedings of the 20th International Conference on Very Large Database，1994：478-499．

　　[4] GOUDA K， ZAKI M J. Efficiently mining maximal frequent item sets[C]. Proceedings of the IEEE International Conference on Data Mining，2001：163-170．

　　[5] ZHOU QH， WESLEY C， LU BJ. SmartMiner. A depth 1st algorithm guided by tail information for mining maximal frequent item sets[C]. Proceedings of the IEEE International Conference on Data Mining， 2002：570-577.

　　[6] GRAHNE G， ZHU J E． High performance mining of maximal frequent item sets[C]. Proceedings of the 6th SIAM International Workshop on High Performance Data Mining，2003：135-143．

　　[7] GRAHNE G， ZHU J F． High performance mining of maximal frequent item sets[C]. Proceedings of the 6th SIAM Int′I Workshop on High Performance Data Mining，2003：135-143．

　　[8] 顏躍進，李舟軍，陳火旺．基于FP-Tree有效挖掘最大頻繁項集[J]．軟件學報，2005，16（2）：216-219．

　　[9] Liu Guimei， Lu Hongjun， Xu Yabo. Ascending frequency ordered prefix-tree：efficient mining of frequent patterns[C]. Proceedings of the 8th International Conference on Database Systems for Advanced Applications， Kyoto， Japan，2003：65-72.

　　[10] 毛宇星，陳彤兵，施伯樂.一種高效的多層和概化關聯規則挖掘方法[J]．軟件學報，2011，22（15）：2965-2980.

　　[11] 陳光鵬，楊育彬，高陽，等.一種基于MapReduce的頻繁閉項集挖掘算法[J].模式識別與人工智能，2012，25（2）：220-224.

　　[12] 胡德敏，趙瑞可.一種改進的最大頻繁項集挖掘算法[J].計算機應用與軟件，2012，29（12）：186-188.