摘 要: 采用基于信號處理領域最近興起的壓縮感知理論對NC-OFDM系統進行信道估計,并將回溯迭代自適應正交匹配追蹤算法(BAOMP)應用到NC-OFDM系統的信道估計中,該算法在每次回溯迭代中核查所選原子的可靠性并刪除不可靠原子。理論分析和仿真實驗表明,BAOMP算法不但可以減少導頻的數目,而且其在保持OMP類算法優點的同時,有著更好的重構性能,且不需要預先知道稀疏度K。
關鍵詞: 信道估計;壓縮感知;NC-OFDM;BAOMP
無線通信中的傳播路徑非常復雜,信號通常會有陰影衰落、頻率選擇性衰落,而且會產生幅度、相位失真等。為了能從接收信號中準確地恢復發送信號,就需要知道信道準確的狀態信息,因此進行信道估計非常有必要。
目前最常用的信道估計方法是基于導頻的信道估計,它通過估計混合在發送數據中的導頻數據的信道響應,然后利用一些插值算法估計出數據的信道響應。這種估計算法已相當成熟,如最小二乘算法(LS)、線性最小均方誤差算法(LMMSE)[1]等。本文在基于導頻的信道估計方法中利用壓縮感知技術對NC-OFDM系統[2]進行信道估計。
壓縮感知(CS)是一種全新的信息采集、編碼及解碼理論[3],其核心思想是當信號具有稀疏性時,將信號的采集、壓縮合并,采集少量的信號投影,然后通過一系列的解碼及信號重構算法實現信號的近似重構,從而降低信號采樣頻率和數據傳輸代價。目前基于貪婪迭代的匹配追蹤算法有MP[4]、OMP[5]、StOMP[6]等,由于這些算法運算量較小且容易實現,因此應用較多。
1 NC-OFDM系統及其信道估計
NC-OFDM是基于認知的OFDM,它與OFDM最大的不同是通過動態的頻譜感知模塊實時檢測周圍的頻譜環境,動態地調整子載波的分配,利用空閑頻譜進行高速的數據傳輸。本文假設信道為頻率選擇性慢衰落信道,其離散時間模型可描述為:

其中,hk和?子k分別為第k條路徑的幅度和時延,L為信道的多徑數。系統采用N點FFT,則接收端的N×1接收信號Y為:
Y=XH+n=XWh+n(2)
其中,N×N矩陣X為用戶數據組成的對角陣,h=[h1,h2,…,hL-1]T為信道沖擊響應向量,N×1向量H為h的N點DFT,N×1向量n為加性高斯白噪聲,自相關矩陣為In。
P×N選擇矩陣S由N×N單位陣與導頻信號所在位置相對應的P行構成,它用來從N個子載波中選出P個導頻信號所在的位置。則在接收端收到的導頻位置上的信號為:
Yp=Xp Hp+np=XpWp h+np(3)
其中,P×1向量Yp=SY;P×P矩陣Xp=SXS′為發送端的導頻信號;P×1向量Hp=[H(n0),H(n1),…,H(nk),…,H(np-1)]T為導頻位置上的信道衰落系數;P×1矩陣Wp=SW;np=Sn為導頻所在位置噪聲。對于接收端,Yp、Xp、Wp均為已知信號,因此接收端通過一定的算法能得到向量h,信道頻域響應可由式(4)得出:
H=Wh(4)
導頻位置上信道估計方法中的最小二乘算法以觀測值與估計值之間加權誤差最小為原則,利用LS估計導頻所在位置的信道頻域響應為:

再以P,LS為基礎,采用線性內插的方式獲得所有子載波上信道頻域響應LS。
2 壓縮感知理論
已知某個信號是稀疏的或可在某個稀疏基下稀疏表示,便可進行壓縮感知。假設一個待壓縮有限長信號x∈CN×1,即x是復數空間C的N×1維列向量,可用N×1維基向量{的線性組合表示,N×N維矩陣的列向量由得到。x可表示為:

其中,h=[h1,h2,…,hN]T為N×1維系數列向量,x和h可看作在不同域上的投影。若h僅有k×N個非零系數,其他都是近似為零的小數值,則稱x是k-稀疏的,?追稱為x的稀疏域。已證明大部分信號都可以在某些變換域上投影為稀疏信號,從而為壓縮感知提供了前提。
根據壓縮感知理論,可將稀疏信號x投影到一組基上,得到M個投影值y,根據這M個投影值y就可以以極大概率恢復出信號x,此時y可表示為;

其中,準為與追不相關的M×N維觀測矩陣,Z=?準?追為M×N維傳感矩陣。接收端利用y的M個元素重建信號x,即從式(7)中求出x向量的N個元素。由于式(7)中未知數數目多于方程組數目,因此x的解不是唯一的。當矩陣Z滿足受限等距條件(RIP)時,方程存在確定解,即對任意?啄∈(0,1),使Z對所有k稀疏信號x均滿足:

在最小l1范數下的最優化問題成為基追蹤算法(BP)[7]。
3 基于壓縮感知的NC-OFDM系統的稀疏度自適應估計算法
傳統的信道估計方法要求采樣值的個數滿足抽樣定理,才能根據式(3)中的采樣向量Yp和導頻符號Xp求解出信號在導頻位置上的頻域響應Hp,之后再進行均衡等步驟完成信道估計。而在壓縮感知中,當采樣向量Yp包含的元素個數小于導頻符號Xp的個數時,依然能夠利用一定的重構算法恢復出Hp。因此,在基于壓縮感知的信道估計中,可利用少量的導頻實現信道估計,使得節省下來的子載波用來傳遞數據信息,提高系統吞吐量。
在壓縮感知的重構算法中,傳統的貪婪迭代算法都不是自適應的,需要預先估計稀疏信號的稀疏度K,而且信號的重建精度也不能讓人滿意。現實中,稀疏信號的稀疏度一般是未知的,為了提高重建精度,使算法具有自適應性,參考文獻[8]提出了BAOMP算法,該算法作為OMP算法的延伸,采用了回溯迭代方法,通過在每一迭代步驟中自適應地從冗余字典中增加或刪除原子,以實現信號的重構。
BAOMP算法首先自適應地選取一些原子,然后在接下來的處理中為了更準確地確定支撐集,使用回溯策略移除某些選擇錯誤的原子,具體步驟如下:
輸入:M×N階觀測矩陣?準,抽樣觀測向量y,預置的[0,1]間增加原子的閾值?滋1,預置[0,1]間刪除原子的閾值?滋2,停止迭代的相關系數?著,所允許的最大迭代次數nmax。

在該算法中,∧是當前迭代的支撐集,?準∧由支撐集∧包含的列所對應的觀測矩陣?準的列向量組成。與大多數OMP類型的算法一樣,該算法的第一步是選擇候選集Cn,約束條件|Cn|≤M-|∧|用于保證的逆矩陣存在。在第二步中,常數?滋2用于自適應控制每次迭代刪除的原子數,這種貪婪算法的目的是尋找信號的k階系數表示,其近似系數最大,從而可以減小誤差。BAOMP算法使用上述回溯方法移除近似系數相對較小的原子,由于k并非是輸入參數,因此BAOMP算法的結束條件是||rn||2<?著或者迭代次數超過最大限值。
BAOMP算法通過回溯的方法修正支撐集,但它不像SP和CoSaMP算法每次增添或刪除固定數目的原子,而是通過當前信號的特征自適應地選擇增添或刪除一些原子。即如果k較小,則較少數目的原子被增添或刪除;如果k較大,則較多數目的原子被增添或刪除。而且BAOMP算法在選擇了大多數的正確原子之后,選擇的原子數目會逐漸變少,會加速收斂,因此BAOMP算法會在算法復雜度和重構精度之間達到很好的平衡。回溯追蹤使BAOMP算法兩次核查所選原子的可靠性,第一次核查是在考慮到觀測向量與殘差的相關性時,第二次是在觀察支撐集∧的近似系數時,回溯調整會帶來更好的稀疏度重構性能。
4 仿真與性能分析
在NC-OFDM系統中,使用MATLAB進行仿真分析,參數如下:可用子載波數為500,授權用戶占用子載波數為100,每一次傳輸信號時可用子載波位置隨機。采用梳狀導頻圖案,導頻圖案在可用子載波間均勻放置。
在本實驗中,分別利用OMP、ROMP、StOMP和BAOMP算法對信號進行重構估計。原始信號是長度N=256的高斯或者二進制稀疏信號,假設采樣點M=128。針對每一個稀疏度K,每個算法都進行500次獨立重構實驗,并統計出其中成功重構的次數,將成功重構的次數除以實驗總次數便可得到成功重構的概率。當原始信號和重構信號的最大數量級差小于10-3時,則認為重構信號是準確的,即xi-x<10-3。

稀疏度K不同的情況下信號的準確重構率如圖1所示。從圖1(a)可以看到,對于高斯稀疏信號,BAOMP算法要優于其他三種算法,其他三種算法的重構率當稀疏度K≥40時開始衰落,然而BAOMP在稀疏度K≤50之前幾乎仍然保持100%的重構率。此外,當原始信號不夠稀疏時,BAOMP算法仍然有較高的重構率,例如當K=65時,其他算法的重構率幾乎為0,而BAOMP的準確重構率依然超過0.6。圖1(b)展示了二進制信號的情況,可見BAOMP的重構性能依然是最好的。
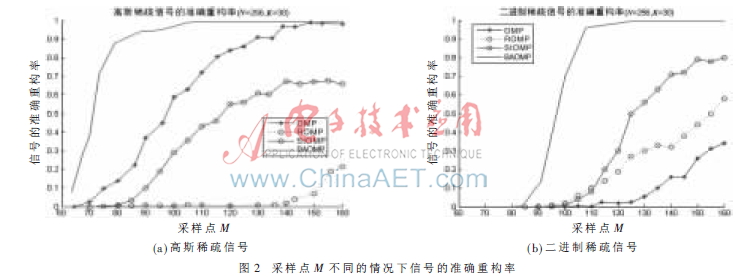
圖2是在稀疏度K=30的情況下,當采樣點M不同時,對信號的準確重構率的影響。實驗步驟類似,仿真結果表明BAOMP有著最好的重構性能。
本文將壓縮感知技術應用到NC-OFDM系統的信道估計中并分析了自適應重構算法BAOMP。與壓縮感知中的OMP類型算法相比,BAOMP算法可以移除先前選擇錯誤的原子,可以比其他OMP類型的算法提供更好的重構性能。實驗表明,BAOMP算法在計算復雜度和重構性能方面可以達到很好的平衡,而且在某些應用中,當稀疏度K未知或者某些貪婪算法預估的K值不能達到預期時,應用BAOMP可以達到很好的重構效果。
參考文獻
[1] KANG S G,HA Y M,JOO E K.A comparative investiga-tion on channel estimation algorithms for OFDM in mobile communications[J].IEEE Transactions on Broadcast,2003,49(2):142-149.
[2] MITOLA J,MAGUIRE G J.Cognitive radio:making softwareradios more personal[J].IEEE Personal CommunicationsMagazine,1999,6(4):13-18.
[3] DONOHO D L,TSAIG Y.Extensions of compressed sensing[J].Signal Processing,2006,86(3):533-548.
[4] MALLAT S,ZHANG Z.Matching pursuits with time-frequ-ency dictionaries[J].IEEE Transactions. on Signal Process-ing,1993,41(12):3397-3415.
[5] PATI Y C,REZAIIFAR R,KRISHNAPRASAD P S.Orthog-onal matching pursuit:recursive function approximation withapplication to wavelet decomposition[C].27th Annual Conf. on Signal and Computers,1993:40-44.
[6] DONOHO D L,TSAIG Y,DRORI I,et al.Sparse solution of underdetermined systems of linear equations by stagewiseorthogonal matching pursuit(StOMP)[J].IEEE Transactions on Information Theory,2012,58(2):1094-1121.
[7] TAUBOCK G,HLAWATSCH F.A compressed sensing tech-nique for ofdm channel estimation in mobile environments: exploiting channel sparsity for reducing pilots[C].IEEE ICASSP,2008:2885-2888.
[8] Huang Honglin,MAKUR A.Backtracking-based matching pursuit method for sparse signal reconstruction[C].IEEE Transactions on Signal Processing Letters,2011,18(7):391-394.

