關沫, 佟彤
沈陽工業大學 信息科學與工程學院,遼寧 沈陽 110870
摘要:為更好地解決多核系統實時任務調度問題,針對基本蟻群算法求解最短路徑過程中容易陷入局部最優的情況,對基本蟻群算法進行了改進。改進算法根據系統的實際情況對概率選擇公式做出調整,同時根據相應策略對信息素進行調整,有效地縮小了信息素之間的差距,有利于跳出局部最優狀態。實驗結果表明,該算法與基本蟻群算法相比在收斂速度和計算最優解方面都有了提高。
關鍵詞:蟻群優化算法;多核系統;實時;任務調度
0引言
隨著程序的時間復雜性的增加和硬件成本的減少,多核系統的利用已經越來越多。同時,實時系統領域的實時控制要求也在日益增加,因而提高系統的實時性能至關重要。在這些系統中,程序被劃分成一些任務映射到一些處理器上,以減少程序的完成時間。在這些架構中最重要的挑戰之一是如何視處理器的數量和處理能力來安排任務,在滿足所有任務的時限要求的前提下,給予外部請求及時的響應,使程序的整體執行時間可以盡量最小化。
目前,已出現很多研究著作對異構多核系統下的實時任務調度提出了一些性能較好的算法及其改進算法。然而,即使在簡化了一些問題的假設后,多核系統的任務調度也是NP(Nondeterministic Polynomial)難題[1]。傳統窮舉法計算復雜度大,耗時長[2],所以至今為止還沒有一種被確定為最優的調度算法。正因如此,很多學者仍在孜孜不倦地追求更優解,也為后來的研究者提供了極大的可改進和可拓展空間。
1多核任務調度
在多核系統中,一個程序被劃分成更小的段,命名為任務分布在處理器上。通過同時運行任務來減少程序的整體執行時間。一個程序的任務之間是有依賴關系的。一些任務需要其他任務所產生的數據。因此,任務之間有約束關系,并且內核之間需要數據通信。在本文中,假定是異構體系結構和完全連接的處理器。
早期的異構多核系統大部分是通過啟發式算法解決任務調度問題的,一般是結合最早完成時間(makespan)[3]、最少完成時間和負載均衡等指標,通過使用貪婪算法的思想去求解任務分配的次優解。這種算法雖然收斂速度很快,可是由于所供參考的任務范圍較小,因此比較容易陷入局部最優解[4]。在異構多核系統的任務調度問題中,啟發式算法的局限性導致了人工智能算法的引入,這類算法的主要思想是憑借設定啟發信息去合理引導搜索過程向最優解逐漸收斂,主要有遺傳算法[5]、禁忌搜索算法、鄰域搜索算法、蟻群算法等。它們擅長找到全局最優解,但也普遍存在算法收斂時間較長的缺點,在具體應用過程中很難按基礎算法使用。為了改進人工智能算法,研究者們采用混合調度策略或者設置相關約束條件來不斷加快算法的收斂速度。其中蟻群算法[6]是一種有效的隨機模擬進化算法,它模擬蟻群覓食過程中發現最優路徑的過程,可用于解決組合優化問題。
2基本蟻群算法
蟻群算法是一種人工螞蟻合作來找到一個給定的問題的優化解決方案的并行算法。蟻群算法[7]最早是由DORIGO M等人提出的,靈感來源于大自然中螞蟻尋找食物的群體行為。作為一種解決旅行商問題[8](TSP)的機率型模擬進化算法,它已經成功地應用于許多復雜的離散性優化問題,如二次分配問題(QAP)、車間調度[9](JSP)、車輛路徑、圖著色、排序、網絡路由等。實驗證明該算法能較為出色地解決復雜優化問題,特別是離散性優化問題,是一種比較卓越的優化算法。
下面具體闡述蟻群搜索路徑的原理[10]。如果有一個障礙物,螞蟻要繞過它有兩側兩條路徑,其中一邊的路徑比另一邊長。首先,螞蟻通過隨機運動來繞過障礙。然后,較長一側的信息素蒸發更快,螞蟻逐漸收斂到短的路徑上。因此,它們總是能找到從食物到蟻穴的最短路徑。由上述螞蟻搜索路徑的原理可知,路徑上信息量越大,這條路徑被選中的概率就越大,直到最后,螞蟻完全選中這條路徑,這種現象所體現出的是信息的正反饋機制。
蟻群算法模擬這種覓食行為。在開始時,所有任務的狀態都是可以訪問的,螞蟻被設置為一個初始狀態。它根據相鄰狀態信息素的值使用概率公式選擇下一個任務,并在此路徑上留下信息素,為下一只螞蟻提供可參考信息。使用同樣的方法為任務選擇處理核。螞蟻重復此操作,直到它遍歷過所有的任務。此時,更新任務選擇和處理器選擇路徑上的信息素變量。通過這種機制螞蟻收斂得到最優解。
3蟻群優化算法
為了提高多核系統的調度效率,針對蟻群算法的缺點,從兩方面進行改進:一是在選擇任務和為任務選擇處理核的概率選擇公式的設計上;二是信息素變量的更新。首先,n是給定的任務圖的任務數,處理器的個數為m。τ(i,j)是指有向邊i、j上的信息素變量,η(i,j)是指任務i后會選擇任務j的期望程度。最初所有元素有相同的較小值。然后執行迭代的蟻群算法:
(1)生成蟻群;
(2)設置初始化信息;
(3)每只螞蟻循環(直到完成調度任務)——根據信息素變量選擇下一個就緒任務,為該任務選擇處理器;
(4)記錄信息素變量;
(5)信息素變量的更新。
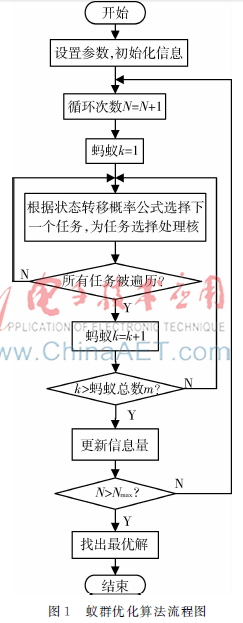
圖1蟻群優化算法流程圖在第一階段,只是創建一個長度為n的列表。在第二階段,每只螞蟻從準備列表中選擇一個任務,并為該任務選擇一個處理核,直到完成任務調度。在每次迭代中,N只螞蟻就會得到N組可行解。選擇一組任務調度長度最短的解作為一次迭代的最優解。對于螞蟻k,通過使用概率選擇式(1)和式(2)為任務i選擇下一個任務j。

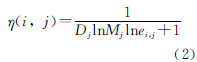
公式的設計考慮如下幾個因素:(1)Dj,任務j的截止期;(2)Mj,任務j的估計運算量;(3)ei,j,任務i和j之間的估計通信量。
在為任務選擇處理器時,根據概率選擇式(1)和式(3)進行選擇。

考慮以下幾個因素:(1)sp,處理核p的處理速率;(2)rj,p,任務j在處理核p上準備就緒的時間;(3)tp,處理核p的最早可用時間。
然后生成一個隨機數,選擇與所生成的數相對應的作為下一個任務。顯然,有較大信息素值的任務有更大的機會被選擇。選定的任務被添加到禁忌表中,
從允許被選擇的列表中刪除,被選擇任務的子任務現在可以執行,增加到準備列表中。這些操作是重復的,直到完成所有任務的調度,換句話說,完成了螞蟻的列表。
在第三階段中,根據k組可行解的情況,對路徑上的信息素變量進行更新,調整策略如式(4)、式(5)和式(6)所示。
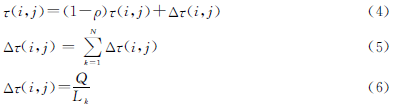
Lk表示第k只螞蟻求得的任務調度長度,Q在基本蟻群算法中是常數,但通過實驗發現,有時會導致搜索停滯,對Q作出兩點改變來解決:一是限定信息素變量的最大值和最小值,二是根據迭代次數對Q值進行調整。
最后階段,選擇所有迭代結束后得到的調度時間最短的解作為最優的解決方案。
4實驗結果及分析
在 Microsoft Visual C++ 60 上使用 C語言實現了本文提出的優化的蟻群算法。用有向無環圖(DAG)對任務進行建模。圖2表示了一個程序的任務圖。
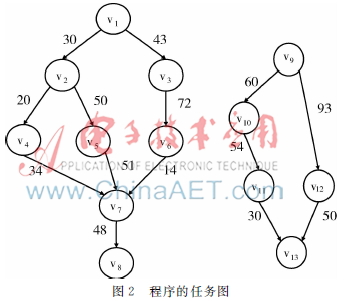
在圖2中,節點是任務,邊是指定任務之間的優先約束。邊(i,j)表明,任務i必須在任務j開始前完成。每個節點的權重是任務的必要的執行時間,邊(i,j)的權重是任務i向任務j傳輸數據所需的時間作為通信成本。如果兩個任務在同一個處理器上執行,它們之間的通信成本將是零。在程序編譯階段產生任務執行時間、通信成本和任務之間的優先級約束。
在實驗中設置參數如下:螞蟻個數為10,最大迭代次數為100,α為2,β為2,ρ為07,該算法成功完成了異構多核系統中的實時任務調度,求出的最優解不僅是可行解,而且任務調度長度較短,充分證明了本文混合算法的可行性。
同時改進蟻群算法與基本蟻群算法進行比較,分析結果如圖3、圖4所示。從圖3可知,改進蟻群算法的平均任務調度長度明顯優于基本蟻群算法;圖4將不同算法得到的最優解進行對比,可知改進蟻群算法得到的最優解的任務調度長度更短并且較穩定,明顯優于基本蟻群算法得到的最優解。

5結論
針對多核系統的實時性,本文算法考慮了任務的到達時間、就緒時間和截止期,再結合多核系統的復雜環境,考慮了各內核不同的運行速率和內核間不同的通信帶寬。將所提出的方法與其他調度方法進行了實驗對比,本文提出的蟻群

優化算法在平均任務調度長度和最優解的任務調度長度上的表現均優于相比較的算法。
參考文獻
[1] CHRETIENNE P, COFFMAN E G, LENSTRA J K, et al. Scheduling theory and its application[J]. Journal of the Operational Research soeiety, 1995,48(7):764765.
[2] Liu Yi, Zhang Xin, Li He,et al. Allocating tasks in multicore processor based parallel system[C]. Proceedings of the IFIP International Conference on Network and Parallel Computing Workshops, Washington DC, 2007: 748753.
[3] Zhu Jie, Li Xiaoping. An effective metaheuristic for nowait job shops to minimize makespan[C]. IEEE Transactions on Automation Science and Engineering, 2012,1(9): 189198.
[4] 劉進,劉春,陳家佳.基于改進蟻群算法的多處理器任務調度仿真[J].計算機仿真,2014, 31( 6):334337.
[5] 王嘉平.多核系統中實時任務調度算法的研究[D].南京:南京郵電大學,2012.
[6] 周會嬌.異構多核系統多媒體流計算實時任務調度策略研究[D].武漢:華中科技大學,2013.
[7] DORIGO M, BIRATTARI M, STUTZLE T. Ant colony optimization [J]. IEEE Computational Intelligence Magazine, 2006, 1(4):2839.
[8] 朱君,蔡延光,湯雅連,等.改進混合蟻群算法求解關聯旅行商問題[J].微型機與應用, 2014, 33(9):8084, 88.
[9] 張麗萍.改進的蟻群算法求解置換流水車間調度問題[J].微型機與應用,2014,33(12):6668,72.
[10] 段海濱. 蟻群算法原理及其應用[M]. 北京: 科學出版社, 2005.

