0 引言

　　近年來，正在進行和已經完成的巡天項目(例如：SDSS巡天[1]、VLT/VIRMOS巡天[2]、VST巡天[3]等)為研究宇宙的起源與演化提供了大量豐富的數據資源。海量數據將帶來許多實質性的挑戰，例如怎樣記錄、加工原始數據；怎樣通過現代計算機硬件和網絡系統存儲、合并、獲取數據；怎樣快速有效地探索及分析數據并將這些數據可視化。運用數據挖掘技術從海量數據中發現稀有的天體或現象，或者根據數據來區分不同類型的天體，這對天文學發展是至關重要的。近年來，測光紅移己經廣泛地應用到天文學許多領域的科學研究上，并己迅速成為觀測宇宙學研究的重要工具[4]。然而，對于SDSS巡天而言，它提供了五億多個星系的精確測光數據，卻只對其中三百萬個星系進行了光譜觀測，獲得了這些星系的光譜紅移，對于其他無光譜觀測的星系的紅移如果能找到行之有效的方法，利用SDSS大量的測光數據估測星系的紅移，這將對研究星系的形成與演化具有劃時代的意義。Hadoop是當前發展較快的一個基于內存的開源分布式計算集群平臺，具有快速、通用、簡單等特點，在迭代式機器學習算法和交互式數據挖掘應用方面具有極高的效率。盡管Hadoop在數據挖掘應用問題上具有明顯的優勢，但至今仍未有講其應用于海量天文數據中的實例。本文將結合斯隆數字巡天最新公布的數據集SDSS-DR12，探索Hadoop平臺下的數據挖掘技術在測光紅移估值中的適應性和應用問題。

1 測光紅移

　　“測光紅移”并不是一個新名詞，它最早出現在PUSCHELL J J等人1982年的文章中[5]。PUSCHELL J J利用寬帶測光數據估測暗射電星系的紅移。LOH E D和SPILLAR E J 1986年第一次在文章題目(Photometric Redshifts of Galaxies)中使用了“測光紅移”的字樣[6]。在20世紀30年代末，D′ABRUSCO R就已經從理論上證明可以根據星系光譜在5 000 ?魡附近的傾斜度估算紅移[7]。但真正將多波段測光方法應用到紅移估測工作中的是BAUM W A，1957年，BAUM W A提出利用測光數據研究紅移，并于1962年開發了一種估計測光紅移的算法[8]。時至今日，神經網絡、隨機森林方法、貝葉斯等數據挖掘算法都已經成功地應用到測光紅移估值中[9-11]。盡管許多研究者對數據挖掘方法估算測光紅移問題進行了比較深入的探索和研究，但受制于當時的技術條件，他們都只注重提高測光紅移估算的精度問題，而忽略了測光紅移估值模型的訓練時間問題。尤其是隨著大型巡天項目的發展，測光數據量急劇增長，如何在大數據集條件下提高測光紅移估值的精度，同時大大降低估算模型的訓練時間，使得能近乎實時地對測光紅移進行估值，幫助科學家有更多的時間對結果進行分析，這是一個值得讓人探討的問題。本文首次使用了基于Hadoop平臺的數據挖掘技術來解決測光數據量過大而導致的模型難以訓練或訓練時間過長的問題。

2 測光紅移平臺及算法

　　2.1 Hadoop上的數據挖掘技術

　　Hadoop大數據處理框架能夠高效、快速、靈活地對海量數據進行處理。運行在Hadoop上的數據挖掘算法是根據數據在Hadoop平臺上分布式存儲的特點而對傳統的數據挖掘算法進行的分布式并行化改造，使其能夠對分布式的海量數據進行高效的數據挖掘。Mahout是在Hadoop平臺上實現數據挖掘算法的機器學習庫，目前已經集成了感知器算法、邏輯回歸、支持向量機和K均值等多種算法[12]。下面重在闡述MLPQNA算法及其在Mahout上的實現。

　　2.2 MLPQNA回歸模型

　　MLPQNA算法以傳統的神經網絡模型MLP（Multi Layer Perceptron）為結構，QNA（Quasi Newton Algorithm）為學習規則，并已經應用在分類問題上[13]。前饋神經網絡為一系列輸入變量和輸出變量間的非線性映射提供一個總體框架。兩層計算層的前饋神經網絡的數學表示如式(1)所示：

　　多層感知器也可以用圖1表示，如圖所示，輸入層（xi）由與輸入變量數（d）等同的感知器組成，輸出層神經元的數目與輸出變量數（K）相同，網絡可能有任意數目個中間層（通常為一層）。在一個完全連接的前饋網絡中，相鄰層的任意節點都相連。每個連接代表一個自適應的權重（連接強度，范圍在[-1，+1]），每個感知器對輸入的響應由一個非線性函數g表示，稱作激活函數。MLP是由輸入層和兩神經元計算層組成的網絡模型，每一隱藏層的神經元都由一個非線性激活函數表示，數據從輸入層傳輸至輸出層之后估算學習誤差（計算與期望輸出值的均方誤差MSE），反向運用學習規則，調整權重，以期降低誤差函數。在學習周期內，數據重復從輸入端傳送至輸出端，直至一定的迭代次數或誤差低于一個閾值，迭代結束。

　　QNA與傳統牛頓方法的不同在于誤差函數黑塞矩陣計算的不同，傳統牛頓方法用黑塞矩陣來找二次型的平穩點，然而黑塞矩陣并非總能求得且通常復雜難算，先計算函數梯度，進而推導黑塞矩陣，每點w梯度的計算如式(2)：

　　在式(3)條件下，w對應誤差函數的最小值：

　　向量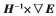稱作牛頓方向，是各種優化策略的基礎。QNA不需要計算H或H-1，用一系列中間步驟以精簡的計算得到一系列矩陣，獲得更精確的黑塞近似。當迭代到第k次，wk和wk+1位于最優化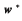鄢附近，H(w)正定，可寫作：

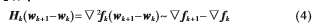
　　假設Ak+1為黑塞矩陣的統計近似，需滿足以下方程式：

　　將MLPQNA算法應用于PHAT1數據集[14]，結果與已知的光譜紅移比較，得出測光紅移的Bias、Scatter、Outliers值，不難發現：與PHAT中幾種機器學習算法比較，無論在18波段還是去除IRAC的14波段，不管對于高紅移還是低紅移的估算，MLPQNA都能獲得最小的Bias值，并且能得到具有競爭力的Scatter值以及離群率。

　　測光紅移估算統計指標：

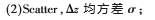
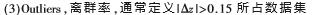
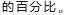
3 測光紅移應用

　　3.1 斯隆數字巡天測光數據集

　　斯隆數字巡天計劃(Sloan Digital Sky Survey，SDSS)是迄今為止最大規模的星系圖像和光譜巡天項目。SDSS同時對天體進行5個波段(u，g，r，i，z)的測量。目前，其最新公布的SDSS-DR12數據容量超過了100 TB，包含了近5億個恒星和星系的精確測光數據和300多萬個天體的光譜數據，為研究各種測光紅移估算算法提供了很好的實驗溫床。在本實驗中，從SDSS DR12 CasJobs中選取了5個波段(u，g，r，i，z)的12個參數作為測光紅移估算的輸入特征，光譜紅移Spectroscopic redshift的值作為期望值來評估Hadoop中的數據挖掘算法，所選用的參數如表1所示(2 619 593條數據記錄，共1.8 GB數據量)。

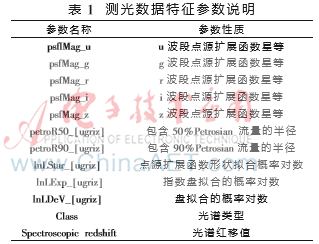
　　3.2 算法參數設置優化與測光紅移估算

　　按照監督學習的慣例，提取3個不相交的子集(訓練集、驗證集、測試集)對Mahout下實現的MLPQNA算法進行評估, 并在使用相同的訓練集和測試集的條件下測試算法的內部參數集對估算結果的影響，以選擇最優的內部參數用于測光紅移估算，獲得每個參數的最優設置值。基于這個方法，選定的MLPQNA最優內部參數如表2所示。

根據表2所獲得的MLPQNA所需的最優內部參數值，在Hadoop集群上測得在整個數據集上估值所需時間、均方差和離群率的結果如表3所示，測光紅移與光譜紅移的對比如圖2所示，MLPQNA與其他機器學習算法估算結果比較如表4所示。從表3中看到，基于Hadoop集群的MLPQNA算法能很好地應用于測光紅移估算問題當中，在數據量高達1.8 GB的情況下，僅僅依靠具有5個計算節點每個計算節點內存為1 GB的Hadoop集群，就能使數據處理時間縮短到幾分鐘之內，而同樣數據集用Weka下的感知器算法對測光紅移估算時，花費了2 h。相比之下，Hadoop下的數據挖掘算法比Weka的感知器算法能更好地適用于具有大數據集的測光紅移估算任務。

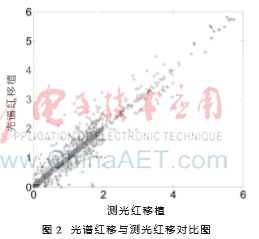
　　3.3 Hadoop 集群節點數量對測光紅移估算性能的影響

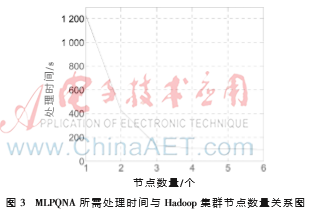
　　在Hadoop集群上，將測光數據集分為訓練集和測試集兩部分，通過逐漸增加集群節點的數量來研究集群節點的數量對估算測光紅移所需時間、測光紅移估算誤差（Bias）與離群率（Outliers）的影響。研究結果如圖3、圖4、圖5所示。從圖4和圖5中可以看出，Hadoop集群中節點數量的變化對測光紅移估算誤差、離群率影響不大，但對測光紅移估算所需的時間影響很大（見圖3）。在一定范圍內，Hadoop集群中節點數量越多，紅移估算所需的時間越少。在集群中的節點數量增加的過程中，測光紅移估算所需的時間有一個急速下降的過程，最后到達一個谷值而幾乎保持不變。測光紅移估算所需時間急速下降的過程正是由于數據挖掘算法并行化使得數據處理的速度得到了提升，然而，估算所需時間降到一定程度而不能再下降則是由于受到網絡傳輸帶寬、計算機內存受限等因素的制約。

4 結論

　　Hadoop分布式平臺作為一種新型高效的大數據處理模型，為數據挖掘技術在觀測天文學中的應用提供了新的有效工具。本文基于最新的斯隆數據巡天測光及光譜數據集，通過對參數空間的探索和代碼的改寫將MLPQNA實現在Hadoop上的機器學習庫Mahout中，在估測測光紅移的實驗中，與PHAT中幾種機器學習算法比較，無論在18波段還是去除IRAC的14波段，不管對于高紅移還是低紅移的估算，MLPQNA都能獲得最小的Bias值，并且能得到具有競爭力的Scatter值以及離群率。因此基于Hadoop 的數據挖掘算法能很好地解決海量天文測光紅移估值問題。并且，隨著Hadoop集群中參與計算節點數量的增加，在保證了測光紅移估算誤差、離群率基本不變的同時，MLPQNA模型的訓練速度和最終測光紅移的估算速度得到了大大的提高，這必將使觀測天文學的各項研究更為高效地開展。

　　參考文獻

　　[1] YORK D G，ADELMAN J，ANDERSON J E，et al.The Sloan digital sky survey：Technical summary[J].Astron.J.，2000，120(3)：338-347.

　　[2] FEVRE L，VETTOLANI G，MACCAGNI D，et al.VirmosVLT deep survey[C].Astronomical Telescopes & Instrumentation，2003，4834：173-182.

　　[3] CAPACCIOLI M，ARNABOLDI M，MANCIN D，et al.The VST-VLT survey telescope[C].Instrumentation and Measurement Technology Conference，1999，2：776-781.

　　[4] 王丹，張彥霞，趙永恒，等.測光紅移算法概述[J].天文學進展，2008，26(3)：266-277.

　　[5] PUSCHELL J J，OWEN F N，LAING R A.Near-infrared photometry of distant radio galaxies-Spectral flux distributions and redshift estimates[J].Astrophysical Journal，1982，257(6)：57-61.

　　[6] LOH E D，SPILLAR E J.Photometric redshifts of galaxies[J].Astrophysical Journal，1986，303(1)：154-161.

　　[7] D′ABRUSCO R，STAIANO A，LONGO G，et al.Mining the SDSS archive.I.Photometric redshifts in the nearby universe[J].Astrophysical Journal，2007，663(2)：752-764.

　　[8] BAUM W A.Photoelectric magnitudes and red-shifts[C].Proceedings from IAU Symposium no.15.New York，USA：Macmillan Press，1962：390.

　　[9] COLLISTER A A，LAGAV O.ANNZ：Estimating photometric redshifts using artificial neural networks[J].Astrophysics，2004，116(818)：345-351.

　　[10] CARLILES S，BUDAV′ARI T，HEINI S，et al.Random forests for photometric redshifts[J].Astrophysical Journal.，2010，712(1)：511-515.

　　[11] WOLF C.Bayesian photometric redshifts with empirical training sets[C].MNRAS，2009，397(1)：520-533.

　　[12] 張明輝，王清心.基于Hadoop的數據挖掘算法的分析與研究[D].昆明：昆明理工大學，2012.

　　[13] BRESCIAL M，CAVUOTI S，PAOLILLO M，et al.The detection of globular clusters in galaxies as a data mining problem[J].MNRAS，2012，421(2)：1155-1165.

　　[14] HILDEBRANDT H，ARNOUTS S，CAPAK P，et al.PHAT：Photo-z accuracy testing[J].A&A，2010，523(A31)：1-21.