文獻標識碼: A
文章編號: 0258-7998(2011)12-0110-04
可靠性和有效性是通信系統必須考慮的兩個主要因素,無線通信還需要考慮頻譜效率和功率效率,對于對抗性無線通信,還希望獲得更好的抗干擾性和低截獲性。截獲最基本的前提是信號強度足夠,也就是說,到達截獲系統天線處的信號必須要達到一定的功率密度,降低通信所需的發射功率能夠在同等條件下獲得更好的低截獲性,同時,采用更低的發射功率完成通信對無線設備的能量損耗也具有重要意義。信道編碼能夠提高通信的可靠性,在同樣的信噪比情況下,獲得更低的誤碼率,也就是說,在同樣條件下,能夠采用更小的發射功率實現同樣的誤碼率,因此能夠具有更好的功率效率和低截獲性能,但同時又因為增加了信息的冗余位而犧牲了一定的頻譜利用率。因此,需要在功率利用率和頻譜利用率之間尋找一個平衡,先進的編碼技術與高效的調制技術相結合能夠有效解決這一難題。對于實際應用而言,可實現性是一個更為重要的因素,因此,如何降低系統中所采用技術的算法復雜度來提高可實現性也是系統設計所要考慮的一個重要問題。本文從串行級聯編碼理論入手,綜合考慮系統的功率效率、頻譜效率和可實現性,在對LDPC和CPM編譯碼算法進行簡化的基礎上,提出了一種新的串行級聯編碼調制系統的設計方案,并對該系統的性能進行了仿真和對比分析,最后,給出了具體實現時硬件資源的使用情況。
1 CPM與LDPC簡介
連續相位調制(Continuous Phase Modulation)是一種包絡恒定、相位連續的調制方式,具有較高的頻譜利用率和功率利用率。這種調制最大的特點就是它的相位連續,從而降低了信號的頻譜旁瓣,使能量主要集中在主瓣中,同時由于其相位具有記憶性,使得該調制方式具有一定的編碼增益。恒包絡特性使得該調制方式對功放的非線性不敏感,尤其適用于需要使用非線性功率放大器的無線通信系統,在遠距離通信中有很大優勢。基于該調制的無線通信系統早在20世紀90年代就已應用于美國的軍方系統。
低密度奇偶校驗碼(Low Density Parity Check Code)是一種分組碼,它是一種性能優良的信道編碼,在中長碼時有著優于Turbo碼的性能,能夠獲得距離香農限零點幾分貝的良好性能,該碼的校驗矩陣很稀疏,因此譯碼復雜度比Turbo碼更低,并且可以實現并行譯碼,減小譯碼時延。目前已被廣泛應用在通信、廣播、HDD硬盤等領域。
1966年FORNEY G D提出了一種串行級聯編碼方案[1],級聯編碼是指可以對信息序列先進行一種編碼(外碼),然后再對外碼編碼所得序列進行另一種編碼(內碼)。Forney的研究表明級聯編碼能夠獲得較大性能改善,使譯碼錯誤概率隨著碼長呈指數減少,而譯碼復雜度只是以代數形式增加。
2 基于LDPC的CPM調制系統模型
根據Rimoldi的研究[2],CPM可以分解為連續相位編碼器(Linear Continuous Phase Encoder)和無記憶調制器(Memoryless Modulator)兩部分,其中CPE可以看做碼率為1的卷積碼,因此可以作為內碼與其他信道編碼的級聯。通常,在級聯編碼系統的外碼和內碼之間加入一個交織器,可以大大提高性能。但是,由于LDPC本身的內在交織性使得經過編碼的LDPC碼已經具有類似于交織器的打亂順序的特點,所以在LDPC與CPM級聯的系統中交織器不是必須的。因此,本文提出了如圖1所示的基于LDPC編碼的CPM調制系統模型。
在發射端,需要發送的信息字經LDPC編碼后進行符號映射,然后輸入到M進制的CPM中,CPE部分對輸入信息進行連續相位編碼,編碼后獲得的相位經過MM調制器調制后發射出去。
在接收端,采用基于SISO算法的CPM譯碼器進行硬判決并輸出符號的軟信息。CPM軟譯碼器對每個時刻可能碼字符號的概率進行比較判決,并將這個符號的概率作為似然概率輸出,對LDPC譯碼器進行初始化。經LDPC譯碼模塊進行迭代譯碼后作硬判決輸出。
3 系統的工作過程
3.1 系統的編碼調制過程
鑒于LDPC碼編譯碼算法的復雜度較高,直接使用將帶來較高的編譯碼時延,會給工程實現增加難度。因此,在系統設計時,采用了準循環LDPC(Quasi Cyclic LDPC)碼[3],該碼的準循環特性使得該碼在編譯碼上具有規律性,可采用簡單的移位寄存器實現,能夠有效降低譯碼復雜度。
QC-LDPC的編碼采用了RICHARDSON等人提出的“貪婪算法”[4],該算法通過對行滿秩的校驗矩陣H進行行列置換,變換成近似下三角形式,同時將H劃分為幾個小塊的稀疏矩陣,然后再進行編碼,對矩陣的行列置換保持了矩陣的稀疏性,降低了編碼的復雜度,實現了近似線性編碼,在實際工程中得到了較為廣泛的應用。
3.2 系統的解調譯碼過程
參考文獻[6]設計的LDPC+CPM串行級聯系統采用了兩譯碼器之間信息互相傳遞并進行迭代,直到LDPC碼譯碼器譯碼成功或者達到最大迭代次數后判決輸出。這種設計基于LDPC與CPM兩種譯碼算法之間相互迭代和傳遞消息,雖然較本文的系統結構會有一定的性能優勢,但卻極大地增加了譯碼復雜度,帶來了惡劣的處理延時和存儲空間問題,實際應用中硬件實現困難。因此經仿真分析并權衡性能和可實現性后提出了圖1所示的系統結構,這樣的結構不需要在LDPC和CPM兩者之間進行迭代譯碼,使得系統能夠獲得更快的譯碼速度和更少的數據存儲。
如圖1所示,CPM調制后的信號經過信道后,在接收端同本地存儲的所有發射基帶波形進行匹配相關,并將相關值作為似然信息送入CPM的SISO譯碼器進行一次迭代更新。CPM譯碼迭代采用的是基于BCJR算法的SISO譯碼方法[7],輸出更新后的模板匹配最大值。通過此最大值,可以確定其所對應的C,而所存模板中每一個C對應的“當前時刻”的輸入信息符號un是確定的。由此,經匹配相關可確定un。再將un分解為原信息比特,并通過相關峰值獲取每一信息比特的初始消息,傳遞給QC-LDPC譯碼器進行譯碼迭代。

由于置信傳播(Belief-propagation)算法在橫向迭代過程中需要大量的乘法運算,復雜度較高。因此,系統中的QC-LDPC譯碼采用了歸一化的最小和譯碼算法(Normalized Min-Sum Decoding Algorithm)[8],該算法在橫向迭代過程中,采用近似算法,將橫向迭代簡化為數值比較過程,即將非線性關系變換為線性關系,從而減小了譯碼復雜度,同時通過調整比例系數,在非線性關系變換為線性關系的過程中增加BP算法和MSA兩種算法間的運算擬合度,從而降低誤差。經LDPC譯碼后判決并輸出譯碼后的信息。
4 性能仿真與分析
為檢驗所設計系統的性能,對不同級聯方式系統的誤碼性能進行了Matlab仿真。仿真中采用加性高斯白噪聲(AWGN) 信道模型。各方案的具體參數見表1。

其中,LDPC碼選用CCSDS提供的碼率R=2/3,信息位k=1 024的QC-LDPC碼,SCCPM系統中CC(3,[5,7])編碼交織長度為1 024,單個符號采樣點相同fs=11。仿真結果如圖2和圖3所示。

由圖2可以看出,在同樣CPM調制參數下,本文設計的LDPC+CPM系統誤碼性能要優于SCCPM系統。SCCPM的錯誤平層現象[9]在圖2中有所體現,因為SCCPM譯碼器采用類似于Turbo碼的迭代譯碼從而獲得非常好的誤碼性能,但是又由于其外碼為自由距離非常小的卷積碼,使得大約在10e-6時誤比特率隨著信噪比增加開始緩降。而LDPC具有瀑布區,在EbN0=1.5~2.5 dB之間誤碼性能隨信噪比增加急劇提升。
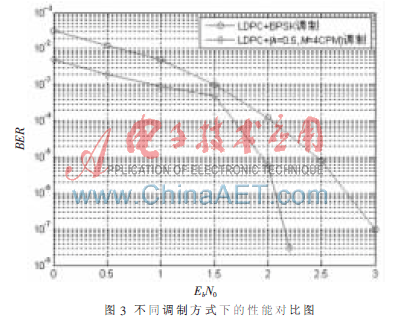
由圖3可以看出,在同樣的編碼下,LDPC+CPM系統的性能要優于LDPC+BPSK系統。LDPC+BPSK系統中,首先經過BPSK解調將其作為LDPC譯碼的初始似然信息,然后LDPC譯碼器進行迭代譯碼。LDPC+CPM系統中,首先進行CPM的解調譯碼,這相當于G.D.Forney模型中的內碼譯碼,然后將譯碼軟信息傳遞到LDPC譯碼器中進行第二級譯碼,顯然級聯碼系統具有更好的性能。如圖所示,LDPC+CPM較LDPC+BPSK方式在10e-6的誤碼層面上需要的信噪比大約減少0.7 dB,相當于CPM調制提供了約0.7 dB的編碼增益,這一結果與FORNEY G D的研究理論也是相符合的。
5 硬件實現情況
系統的實現采用了DSP+FPGA架構,其中DSP主要負責完成系統數據流的控制,FPGA負責完成QC-LPDC碼的編譯碼算法及CPM調制的調制解調,模板匹配所用模板的存儲等[10]。
FPGA芯片選用的XILINX公司VIRTEX-5系列的XC5VSX95T。經ISE軟件編程仿真通過后,得到的FPGA芯片資源使用報告如圖4所示。

可以看到,乘法器資源占用率只有23%,這表明文中對系統結構的優化設計及主要算法的近似簡化能夠有效減少編譯碼時的運算量,降低了對硬件資源的需求。
CPM是一種具有很多優點的先進調制技術,其優秀的功率譜性能以及恒包絡特點使得該調制技術非常適用于遠距離無線通信,相對于其他級聯方式的系統設計,基于LDPC的CPM調制系統能夠采用更小的發射功率來完成同等距離上的無線通信,這對于對抗性無線通信的低截獲性需求具有非常重大的意義。從可實現性角度出發,對編碼和調制的編譯碼算法進行簡化,減少乘法運算,將非線性運算通過合理近似轉換為線性運算,從而降低各算法的實現復雜度。通過分析比較,優化系統結構,取消LDPC編碼和CPM調制之間的迭代運算,以犧牲較小的性能為代價,換得更小的譯碼延時和更少的資源需求,降低系統的實現復雜度,使得整個系統能夠在一片FPGA中得以實現,這對于現實應用具有重要的參考價值和指導意義。
參考文獻
[1] FORNEY G D, Jr. Concatenated Codes[M]. M.I.T.Press, Cambridge, MA, USA, 1966.
[2] RIMOLDI B E, A decomposition approach to CPM[J].IEEE Trans. Inf. Theory, 1988,34(2):260-270.
[3] FOSSORIER M P. Quasi-cyclic low-density parity-check codes from circulant permutation matrices [J]. IEEE Transactions on Informatron Theory, 2004(50):1788-1793.
[4] RICHARDSON T J, URBANKE R. L. Efficient encoding of low-density parity-check codes[J]. IEEE Transactions on IT, 2001,47(2):638-656.
[5] AULIN T, SUNDBERG C E W. Continuous phase modulation Part I[J].IEEE Trans. Comm, 1981(29):196-225.
[6] 薛睿,趙旦峰,肖春麗.基于Turbo迭代算法的LDPCC-CPM系統接收機設計[J].深圳大學學報(理工版), 2010,27(3):301-305.
[7] PAPAHARALABOS S, SYBIS M, TYCZKA et al. Modified Log-Map algorithms for simplified decoding of turbo and turbo TCM codes[J]. VETECS., 2009,69(3):1-5.
[8] Chen Jinghu, DHOLAKIA A, Hu Xiaoyu, et al. Reduced complexity decoding of ldpc codes [J]. IEEE Trans. on Commun., 2005,53(8):1288-1298.
[9] 張敏,黃俊偉,孟杰.CMMB中LDPC碼的編譯碼研究及仿真性能分析[J].電子技術應用,2009,35(9):112-115.
[10] 賈哲,鄭翔.一種四進制CPM調制器的設計與FPGA實現[J].電訊技術,2006,46(5):153-155.

