摘 要: 針對(duì)核脈沖全譜數(shù)據(jù)采集技術(shù)中采用的深度加權(quán)濾波法在數(shù)據(jù)量少時(shí)平滑效果差、滯后大的缺點(diǎn),設(shè)計(jì)了卡爾曼濾波算法替代傳統(tǒng)濾波算法進(jìn)行解譜的方案。濾波算法首先根據(jù)信號(hào)與噪聲的狀態(tài)空間模型,建立狀態(tài)方程和測(cè)量方程,然后根據(jù)廣義卡爾曼濾波對(duì)測(cè)量方程進(jìn)行更新,最后根據(jù)現(xiàn)場(chǎng)的標(biāo)準(zhǔn)刻度井測(cè)量數(shù)據(jù)確定測(cè)量矩陣,對(duì)測(cè)量數(shù)據(jù)進(jìn)行濾波。實(shí)測(cè)結(jié)果表明,該濾波算法相對(duì)于傳統(tǒng)濾波算法,能夠消除譜圖的統(tǒng)計(jì)漲落,提高光滑度,遏制滯后,并保證濾波后曲線不失真。
關(guān)鍵詞:卡爾曼濾波;數(shù)據(jù)處理;核脈沖全譜數(shù)據(jù)采集系統(tǒng);解譜
0 引 言
核脈沖全譜數(shù)據(jù)采集技術(shù)是新一代放射性測(cè)井儀器的核心技術(shù)。由系統(tǒng)的放射源發(fā)出662 kev γ射線,在地層中經(jīng)過一次或多次的康普頓散射和光電效應(yīng),經(jīng)物理探測(cè)窗口進(jìn)入NaI晶體,產(chǎn)生與入射能量成正比例的光電信號(hào)。 光電信號(hào)經(jīng)光電倍增管形成核電子脈沖信號(hào)。核脈沖信號(hào)A/D轉(zhuǎn)換,分道測(cè)量計(jì)數(shù)[1],上傳地面計(jì)算機(jī),形成全譜數(shù)據(jù)譜線。由于計(jì)數(shù)器存在嚴(yán)重的統(tǒng)計(jì)漲落,必須去偽存真,以便資料分析。
其信息處理技術(shù)的關(guān)鍵是實(shí)測(cè)譜的解析技術(shù)。解譜方法采用深度加權(quán)濾波法。公式如下:
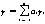 (1)
(1)
其中,y是n個(gè)采樣值的加權(quán)平均值,yi是加權(quán)因子,ai是加權(quán)系數(shù),各個(gè)加權(quán)系數(shù)均為小于1的小數(shù),且滿足總和等于1的約束條件。計(jì)算雖然簡(jiǎn)單,但是需確定歸一化因子的值,即需要確定ai的值,且在數(shù)據(jù)量少時(shí)平滑效果差、滯后大。
本文設(shè)計(jì)的卡爾曼濾波能夠消除譜圖的統(tǒng)計(jì)漲落,提高光滑度,遏制滯后,實(shí)現(xiàn)測(cè)井?dāng)?shù)據(jù)的有效濾波。
1 卡爾曼濾波的模型建立
1.1 建立系統(tǒng)的狀態(tài)方程
卡爾曼濾波以最小均方誤差為估計(jì)的最佳準(zhǔn)則,以此來尋求一套遞推估計(jì)的算法,其基本思想是:采用信號(hào)與噪聲的狀態(tài)空間模型,利用前一時(shí)刻的估計(jì)值和現(xiàn)時(shí)刻的觀測(cè)值來更新對(duì)狀態(tài)變量的估計(jì),求出現(xiàn)時(shí)刻的估計(jì)值。它適合實(shí)時(shí)處理和計(jì)算機(jī)運(yùn)算[2]。
卡爾曼濾波注重對(duì)象的物理過程描述,要求先建立系統(tǒng)的狀態(tài)方程,由于地層的變化是未知的,很難用一組確定的微分方程加以描述,因此采用一階高斯馬爾科夫過程描述地層變化。
首先設(shè)核脈沖個(gè)數(shù)α和每道脈沖能量β為狀態(tài)變量(X1,X2)[3],有:
 (2)
(2)
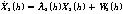 (3)
(3)
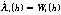 (4)
(4)
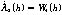 (5)
(5)
式(2)~式(5)中,h表示井的深度,λ1(h)、λ2(h)是非奇異狀態(tài)轉(zhuǎn)移矩陣,是隨井深變化的斜率參數(shù)。W1(h)~W4(h)是動(dòng)態(tài)噪聲,方差為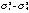 ,均值為零。
,均值為零。
參數(shù)λ1(h),λ2(h)是局部隨機(jī)變化的。若測(cè)井井段類似于均勻的地層區(qū),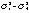 f取得足夠小時(shí),λ1(h)、λ2(h)趨于零,則有
f取得足夠小時(shí),λ1(h)、λ2(h)趨于零,則有 當(dāng)測(cè)井井段跨越一個(gè)地層界面時(shí),λ1(h)、λ2(h)根據(jù)X1(h)、X2(h)的變化斜率取正值或負(fù)值。若把λ1(h)、λ2(h)設(shè)為增廣狀態(tài)變量X3(h)、X4(h),則狀態(tài)方程可表示為:
當(dāng)測(cè)井井段跨越一個(gè)地層界面時(shí),λ1(h)、λ2(h)根據(jù)X1(h)、X2(h)的變化斜率取正值或負(fù)值。若把λ1(h)、λ2(h)設(shè)為增廣狀態(tài)變量X3(h)、X4(h),則狀態(tài)方程可表示為:
 (6)
(6)
f表示式(2)~式(5)的非線性關(guān)系。式(6)描述了地層隨井深的變化,同時(shí)還需要建立反映測(cè)量信息與狀態(tài)變量間的對(duì)應(yīng)關(guān)系的測(cè)量方程。
1.2 最優(yōu)測(cè)量方程的建立
設(shè)長(zhǎng)、短道源采集的核脈沖的個(gè)數(shù)X1(h)和每個(gè)脈沖的能量X2(h)的測(cè)量計(jì)數(shù)率為Z(h),設(shè)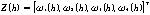 ,則其關(guān)系可表示為:
,則其關(guān)系可表示為:
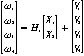
(7)
由于增廣的狀態(tài)為4個(gè),最后測(cè)量矩陣為4×4階矩陣。
測(cè)量方程為:
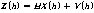 (8)
(8)
式(7)反映了狀態(tài)變量式(6)與測(cè)量方程式(8)之間的對(duì)應(yīng)關(guān)系。由于狀態(tài)方程式(6)是非線性的,而測(cè)量方程式(8)是線性的,所以需要采用廣義卡爾曼濾波對(duì)測(cè)量方程(8)進(jìn)行濾波更新。
下面用狀態(tài)方程和系統(tǒng)測(cè)量方程結(jié)合它們的協(xié)方差來估算系統(tǒng)的最優(yōu)化輸出。利用過程模型來預(yù)測(cè)下一狀態(tài)的系統(tǒng)。假設(shè)現(xiàn)在的系統(tǒng)狀態(tài)是k,根據(jù)系統(tǒng)的模型,可以基于系統(tǒng)的上一狀態(tài)而預(yù)測(cè)出當(dāng)前狀態(tài)[4-5]:

式(9)中,狀態(tài)微分方程組右端項(xiàng);T表示系統(tǒng)的采樣間隔;其中:
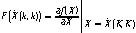 (10)
(10)
至此,系統(tǒng)結(jié)果已經(jīng)更新了,對(duì)應(yīng)于的協(xié)方差的更新如下(用P表示協(xié)方差):
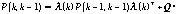 (11)
(11)
式(11)中Qn表示 W(k)動(dòng)態(tài)噪聲的協(xié)方差矩陣;λ(h)T表示λ(h)的轉(zhuǎn)置矩陣,且:
 (12)
(12)
其中,I為單位矩陣。
式(9)、式(11)即是對(duì)系統(tǒng)的預(yù)測(cè)。
結(jié)合當(dāng)前狀態(tài)的預(yù)測(cè)值和當(dāng)前狀態(tài)的測(cè)量值,得到現(xiàn)在狀態(tài)k的最優(yōu)化估算值X(k,k):
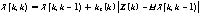 (13)
(13)
式(13)中,kg表示卡爾曼增益(Kalman Gain):
 (14)
(14)
式(13)、(14)中,H表示測(cè)量矩陣;Rm表示測(cè)量噪聲的協(xié)方差矩陣。
為使卡爾曼濾波器不斷地運(yùn)行下去直到系統(tǒng)過程結(jié)束,再對(duì)k狀態(tài)下X(k,k)的協(xié)方差進(jìn)行如下更新:
 (15)
(15)
式(9)~式(15)是對(duì)測(cè)量方程(8)的濾波更新,即得到最優(yōu)測(cè)量方程。結(jié)合式(6)~式(8)以及設(shè)定的參數(shù)即可對(duì)譜圖進(jìn)行濾波。
2 測(cè)量方程的參數(shù)設(shè)計(jì)
以上遞推公式中,需要設(shè)計(jì)式(7)以及式(9)~(15)中的參數(shù)。式(7)中,V1~V4為測(cè)量噪聲,H矩陣為4×2階測(cè)量矩陣,可由現(xiàn)場(chǎng)的標(biāo)準(zhǔn)刻度井測(cè)量數(shù)據(jù)來確定。需要說明的是,每個(gè)測(cè)井儀器都有一套自己的H矩陣,它可認(rèn)為是不隨其他因素變化而變化的常數(shù)矩陣。本文中,H1取為:
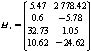
根據(jù)所建立的系統(tǒng)模型式(2)~式(6)以及式(8),對(duì)方程進(jìn)行離散線性化處理,則有:

(16)

(17)

(18)
式(16)~式(18)是式(9)~式(15)的設(shè)計(jì)參數(shù),其中missing image file分別是W1(h)~W4(h)的方差,均值為0。missing image file分別是V1(k)~V4(k)的方差,均值為0。
3 實(shí)測(cè)濾波情況
結(jié)合以上遞推公式,在給定濾波初值(即X(0))后,估計(jì)誤差協(xié)方差矩陣初值P(0,0)、采樣間隔T以及協(xié)方差陣(Qn,Rm),即可以濾波。
在核脈沖全譜數(shù)據(jù)采集系統(tǒng)中,其控制量為儀器中直接貼于NaI晶體端面的一種低強(qiáng)度137Cs源,137Cs源發(fā)射的662 kev射線直接進(jìn)入晶體,γ衰變是核現(xiàn)象,與溫度無關(guān),故與之相對(duì)應(yīng)的電子脈沖信號(hào)應(yīng)維持恒定幅度,并以其為參考值調(diào)整高壓,在譜圖處理中,它可以認(rèn)為是常數(shù)[6],譜圖對(duì)比不受影響。
由于在測(cè)井過程中,儀器運(yùn)動(dòng)速度快,所以核脈沖采集周期一般為20 ms或40 ms。在本文設(shè)計(jì)中,核脈沖的采集周期為40 ms ,即ΔT=40 ms。測(cè)試取一幀的數(shù)據(jù),即256道譜圖。
本文對(duì)實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了處理,在相同的實(shí)驗(yàn)數(shù)據(jù)下,分別對(duì)硫、鋁進(jìn)行測(cè)試對(duì)比,通過長(zhǎng)、短源譜圖濾波,對(duì)卡爾曼濾波譜圖與深度加權(quán)濾波譜圖進(jìn)行比較,具體譜圖波形見圖1~圖4。

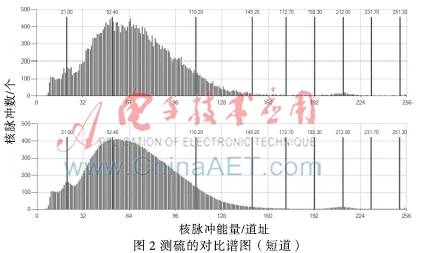
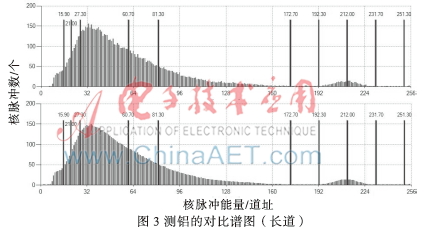
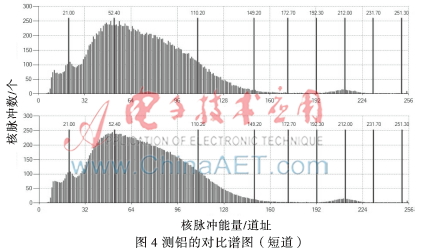
圖1~圖4中,齊的黑線如15.90、27.30等是參考道址,為了方便觀察譜圖是否滯后,便于對(duì)比。道址192.30~265之間是穩(wěn)譜峰圖,主要是為了增加分布在0~192.30道址之間核脈沖的能量強(qiáng)度,便于突出異同,在計(jì)算解釋譜圖時(shí)會(huì)去掉,計(jì)算不受影響。
圖1~圖4中,上圖是深度加權(quán)濾波得到的譜圖,下圖是卡爾曼濾波得到的譜圖,通過上下圖的對(duì)比可以看出,下圖的包絡(luò)明顯趨向平滑,能夠有效消除統(tǒng)計(jì)漲落的影響。通過兩組對(duì)比可以看出,在相同的實(shí)驗(yàn)數(shù)據(jù)下,此卡爾曼濾波得到的譜圖比深度加權(quán)濾波得到的譜圖包絡(luò)線更接近于平滑,有力消除了譜圖的統(tǒng)計(jì)漲落,更利于測(cè)井?dāng)?shù)據(jù)的分析。
4 結(jié)論
文中通過對(duì)核脈沖全譜數(shù)據(jù)采集系統(tǒng)的解譜需求,設(shè)計(jì)了一種卡爾曼函數(shù)濾波器,通過實(shí)驗(yàn)譜圖對(duì)比可以看出,其包絡(luò)線幾乎接近于平滑,消除了譜圖的統(tǒng)計(jì)漲落,提高了光滑度。說明了本文所設(shè)計(jì)的卡爾曼濾波對(duì)譜圖處理的有效性和可行性。
參考文獻(xiàn)
[1] 彭曉光,柏林,田彥民,等. 基于FPGA的全譜巖性密度數(shù)據(jù)采集系統(tǒng)[J]. 核電子學(xué)與探測(cè)技術(shù), 2012,32(7):758-760.
[2] 邵玉華. 卡爾曼波形估計(jì)在雷達(dá)信號(hào)處理中的應(yīng)用[J]. 黑龍江科技信息, 2012(2):77.
[3] 彭丁聰. 卡爾曼濾波的基本原理及應(yīng)用[J]. 軟件導(dǎo)刊, 2009(11):33-34.
[4] 張永偉,楊鎖昌,張敏,等. 卡爾曼濾波在落點(diǎn)偏差預(yù)測(cè)算法中的應(yīng)用[J]. 中國(guó)測(cè)試, 2012,38(s1):112-113.
[5] 黃亞萍. 基于卡爾曼濾波的抑制NLOS定位算法研究[J]. 電信快報(bào), 2012(4):48-51.
[6] 彭曉光. 新型全譜巖性密度測(cè)井儀的研制[D]. 邯鄲:中船重工718研究所, 2012,44-47.

