文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.10.041
中文引用格式: 張艷萍,姚俊,孫心宇. 一種基于相干波束形成的零陷加寬算法[J].電子技術應用,2015,41(10):150-153.
英文引用格式: Zhang Yanping,Yao Jun,Sun Xinyu. A novel null broadening algorithm based on coherent interference beamforming[J].Application of Electronic Technique,2015,41(10):150-153.
0 引言
波束形成是陣列信號處理中的一個重要研究方向,被廣泛應用于通信、雷達信號處理中[1]。自適應波束形成器能夠自動將主波束對準期望信號方向,將零陷對準干擾方向,從而很大程度地提高系統的輸出信噪比。然而在實際情況中,不可避免的有智能干擾、多徑反射等因素的存在,造成期望信號和干擾信號相干,使傳統系統無法有效消除相干的干擾信號。同時由于干擾擾動或者天線接收平臺發生振動的情況,導致干擾信號移出零陷位置從而不能被有效地消除[2]。這些都將使系統輸出信干噪比嚴重下降。
針對干擾信號與期望信號相關的問題。肖紅俠等[3]提出了一種基于多約束最小均方算法的空域調零技術來抑制相干干擾,Zheng Guimei等[4]提出了一種加權極化平滑算法,但計算量較大。劉張林[5]提出了一種基于空間平滑的算法來去相干。
針對干擾信號發生擾動的問題。MAILLOUX R J[6]和ZATMAN M[7]提出了不同的零陷加寬方法,但兩種方法本質上是相同的。GERSHMAN A B[8]提出了一種在干擾方向施加導數約束從而加寬干擾零陷的方法,但該方法運算量較大。王妙等[9]提出了一種基于降秩共軛梯度法的零陷加寬算法。
本文提出了一種基于前后空間平滑的零陷加寬算法。該算法先利用前后向空間平滑的方法有效去除了相干性,并利用迭代求得最優權矢量。再將迭代求得的最優權矢量作為一個“標準”的輸出權值,利用二次約束的方法使方向圖零陷得到展寬。最后通過計算機仿真,對算法的性能進行驗證。
1 算法描述
1.1 陣列結構與信號模型

圖1為M元均勻直線陣列,陣元間距為d(d=?姿/2)。假設有K個遠場窄帶信號入射到陣列上((M+1)/2>K),其中包括一個期望信號s0(t)和K-1個未知的干擾信號(其中有n個與期望信號相干)sl(t)(l=1,…,K-1),則第i個陣元在t時刻所接收的數據信號模型可以表示為:
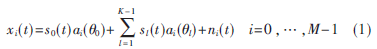
式中:表示第i個陣元對第l個信號的空間響應,ni(t)為第i個陣元上的高斯白噪聲。
陣列的接收信號可表示為:
X(t)=AS(t)+N(t)(2)
式中:X(t)為陣列的M×1維快拍數據矢量,S(t)為信號的K×1維矢量,N(t)為陣列的M×1維噪聲數據矢量,A為空間陣列的M×K維流型矩陣。
當信號源相干時,相干信號源間只差一個復常數,假設有n(n<K-1)個干擾與期望信號相干,第i個相干干擾可以寫為:

將式(3)代入式(2),得相干信號源模型:
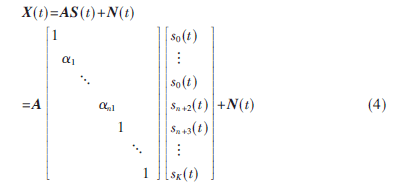
1.2 前后向空間平滑波束形成算法
當期望信號和干擾信號相干時,導致系統不能在所對應的干擾方向形成零陷,干擾不能被有效消除,嚴重影響輸出信干噪比。
本文利用前后向空間平滑技術對期望信號和干擾信號進行解相干處理。將均勻線陣(M個陣元)分成相互交錯的P個子陣,每個子陣所含的陣元數為m=M-P+1,取最左邊的子陣作為參考子陣,如圖2所示。

則第k個子陣有如下數據模型:
Xk(t)=[xk(t) xk+1(t) … xk+m-1(t)]=Am D(k-1)S(t)+Nk(t)(5)
式中:Am為子陣的陣列流行,D為每個入射信號在相鄰陣元引起的固定相位差對角矩陣,Nk(t)為第k個子陣上的高斯白噪聲。
則第k個子陣所接收數據的協方差矩陣為:

式中:H為共軛轉置,Rs為協方差矩陣。
則前向空間平滑的協方差矩陣為:
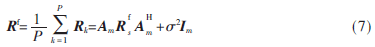
再取最右邊的子陣作為參考子陣,同理,則后向空間平滑的協方差矩陣為:

由于Rb就是Rf的共軛倒序陣,它們之間滿足共軛倒序不變性。因此整個均勻線陣前后空間平滑后的數據協方差矩陣為:

再利用抽樣矩陣梯度算法(Sampling Matrix Gradient,SMG)[10]迭代的方法求取最優權矢量,由約束最小功率準則[11]:

在此約束條件下,使得wHRw最小。式(10)中:w為算法的權矢量,R為入射信號數據協方差矩陣,ad是期望信號導向矢量。
由梯度算法得:

從以上分析可以看出,最陡下降法不需要積累足夠多的快拍數據后再進行權矢量計算,迭代求得最優權值 wSMG。常規的線性約束最小方差算法[11]在求最優權矢量時,計算量為O(M3)。本文采用最陡下降的遞推方法,去除了矩陣求逆,由式(14)可知,計算量為O(M2),運算量降低了一個數量級,有效減少算法運算量。
1.3 零陷加寬
當干擾源快速移動等情況下,都可能使干擾移出方向圖的零陷位置,導致干擾的“欠相消”。本文將迭代求得的最優權矢量wSMG作為一個“標準”的波束形成器的輸出權值,再利用二次約束的方法,得到具有展寬零陷的最優權矢量wopt。

因此本文算法具體步驟如下:
(1)利用前后空間平滑方法得到去相干后的數據協方差矩陣:

(2)利用SMG迭代求取最優權矢量:

(3)將步驟(2)中迭代求得的最優權矢量wSMG作為一個“標準”的波束形成器的輸出權值,再利用二次約束的方法,得到具有展寬零陷的最優權矢量:

2 性能仿真
為了驗證本文方法的正確性和有效性,在計算機上進行仿真實驗。仿真采用15個各向同性的陣元組成的均勻直線陣,子陣列的個數為10,每個子陣列的陣元數為6,快拍數為1 000,蒙特卡羅實驗次數為200次。期望信號的方向為0°,兩個干擾信號的方向分別為-40°(與期望信號相干)和30°,入射信噪比和干噪比分別為SNR=0 dB,INR=30 dB。仿真結果如圖3~圖5。
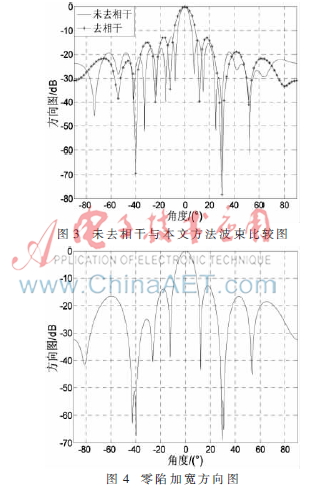
(1)實驗一:方向圖對比仿真
從圖3可以看出,未去相干的波束形成算法只能在非相干干擾方向(30°)形成零陷,而本文的波束形成算法在相干干擾(-40°)和非相干干擾(30°)方向均形成了較深的零陷,較好地抑制了相干干擾。
(2)實驗二:方向圖零陷加寬仿真
其他仿真條件不變,零陷深度系數?著=10-7,仿真結果如圖4所示。
從圖4可以看出,在干擾信號方向-40°和30°處均形成了的零陷。當干擾信號發生擾動時,依然處在零陷范圍內,使得干擾信號能夠較好地被消除。
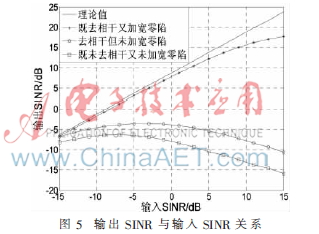
(3)實驗三:輸出SINR與輸入SINR仿真
其他仿真條件不變,輸入信干噪比由-15 dB變化到15 dB,仿真結果如圖5所示。
從圖5可以看出,在相干的干擾信號發生擾動的情況下。既未去相干又未加寬零陷的波束形成算法的輸出SINR損失嚴重。去相干但未加寬零陷的波束形成算法由于干擾信號偏離出了零陷位置,造成輸出SINR下降。而既去相干又加寬零陷的波束形成算法由于相干干擾信號較好的被消除,因此對輸入SINR的變化并不敏感,在輸入SINR整個變化過程中,輸出SINR損失最大約為5 dB。從而進一步驗證了本文方法的有效性。
3 結論
實際環境中不可避免的存在著相干干擾信號和干擾擾動的情況。本文研究了一種在相干信號環境下零陷加寬的方法。通過實驗仿真發現,該方法有效地去除了干擾信號與期望信號之間的相干性。當干擾發生擾動時,仍然能使系統具有較好的輸出SINR。因此本文方法是一種較好的穩健相干波束形成算法。
參考文獻
[1] 張小飛,汪飛,陳華偉.陣列信號處理的理論與應用[M].北京:國防工業出版社,2013.
[2] ZATMAN M.Comments on theory and application of cova-riance matrix tapers for robust adaptive beamforming[J].IEEE Transactions on Signal Processing,2000,48(6):1796-1800.
[3] 肖紅俠,項建弘.基于調零技術的相干干擾抑制方法[J].計算機應用研究,2013,30(6):1779-1782.
[4] Zheng Guimei,Chen Baixiao,Yang Minglei,et al.Weighted polarization smoothing algorithm for electromagnetic vector-sensor array[J].Systems Engineering and Electronics,2012,34(4):637-643.
[5] 劉張林.相干信號源自適應波束形成[J].雷達與對抗,
2011,31(3):23-30.
[6] MAILLOUX R J.Covariance matrix augmentation to producearray pattern troughs[J].Electronics Letters,1995,31(10):771-772.
[7] ZATMAN M.Production of adaptive array troughs by disper-sion synthesis[J].Electronics Letters,1995,31(25):2141-2142.
[8] GERSHMAN A B,NICKEL U,B?魻HME J F.Adaptive beamforming algorithms with robustness against jammer motion[J].Signal Processing,IEEE Transactions on,1997,45(7):1878-1885.
[9] 王妙,方明.一種秩基于降秩共軛梯度法的零陷加寬技術[J].電子信息對抗技術,2011,31(4):1674-2230.
[10] BERTRAND A,MOONEN M,SAYED A H.Diffusion bias-compensated RLS estimation over adaptive networks[J].IEEE Trans. on Signal Processing,2011,59(11):5212-5224.
[11] FROST O L.An algorithm for linearly constrained adaptive
processing[J].Proc.IEEE,1972,60(8):926-935.

