摘 要: 為了提高計(jì)算機(jī)視覺檢測系統(tǒng)的精度與效率,對幾種典型的自動調(diào)焦算法進(jìn)行詳細(xì)對比與分析,提出一種改進(jìn)的新型復(fù)合式自動調(diào)焦算法:首先利用灰度變化率和函數(shù)分段線性插值實(shí)現(xiàn)函數(shù)大范圍快速粗調(diào)焦;再利用梯度向量平方函數(shù)二次插值實(shí)現(xiàn)函數(shù)峰值點(diǎn)附近微小區(qū)域的精確調(diào)焦;對改進(jìn)調(diào)焦算法進(jìn)行測試并做出客觀分析。實(shí)驗(yàn)結(jié)果表明,改進(jìn)后的算法自動調(diào)焦精度高、速度快,且搜索范圍大、通用性強(qiáng),已在數(shù)字刀具測量儀中成功應(yīng)用。
關(guān)鍵詞: 計(jì)算機(jī)視覺檢測;自動調(diào)焦;評價函數(shù);復(fù)合算法;分段線性插值;二次插值
0 引言
在計(jì)算機(jī)視覺檢測系統(tǒng)中,離焦圖像的調(diào)焦質(zhì)量直接影響整個測量系統(tǒng)的性能,只有被測圖像始終保持在CCD鏡頭的焦平面時,才能保證圖像的清晰度和恒定的光學(xué)放大系數(shù),從而保證系統(tǒng)測量的精度與效率。圖像的聚焦程度可通過調(diào)焦算法來衡量,在典型的自動調(diào)焦算法中,高精度與高效率通常是互斥的,難以滿足實(shí)際需要:在較大的調(diào)焦范圍內(nèi)使用較小步長的爬山法時調(diào)焦精度高,但通常需要數(shù)十秒才能獲得滿意的調(diào)焦精度;在小范圍內(nèi)的調(diào)焦速度較快,但難以保證調(diào)焦精度。針對不同典型自動調(diào)焦算法的特性,提出一種復(fù)合式自動調(diào)焦算法,它通過兩種典型自動調(diào)焦算法的有機(jī)結(jié)合,實(shí)現(xiàn)了圖像的高精度、高效率自動調(diào)焦。
1 調(diào)焦判據(jù)與評價函數(shù)分析
1.1 調(diào)焦判據(jù)
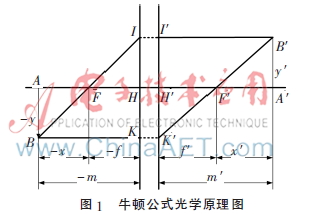
調(diào)焦判據(jù)是一種在光學(xué)系統(tǒng)中判斷調(diào)焦是否滿足物像共軛關(guān)系的標(biāo)準(zhǔn)。根據(jù)牛頓光公式可知,物與共軛面越接近,采集的圖像越清晰;越遠(yuǎn)離,圖像越模糊;當(dāng)物與共軛面重合時,圖像各點(diǎn)間的灰度對比關(guān)系最明顯。這就是實(shí)現(xiàn)調(diào)焦判別的理論依據(jù)。如圖1所示,物方焦點(diǎn)F為原點(diǎn),它到物點(diǎn)的距離為x;像方焦點(diǎn)F′為原點(diǎn),它到像點(diǎn)的距離為x′,物高和像高分別用y和y′表示(圖1采用笛卡兒符號規(guī)則決定正負(fù)方向)[1-3]。
根據(jù)幾何三角形關(guān)系有:
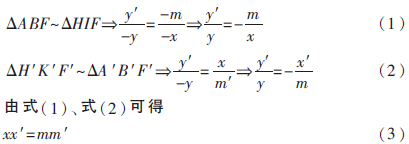
式(3)表示理想光學(xué)系統(tǒng)物、像位置關(guān)系。
1.2 調(diào)焦評價函數(shù)分析
調(diào)焦評價函數(shù)的基本特性:單峰性、半寬度、一致性、靈敏度、響應(yīng)性和穩(wěn)定性。分別用絕對方差函數(shù)、Roberts梯度函數(shù)、梯度向量模方函數(shù)、梯度向量平方函數(shù)、Brenner函數(shù)、拉普拉斯函數(shù)、Tenengrad函數(shù)、均方差函數(shù)與灰度變化率和函數(shù)在相同環(huán)境中處理同一組圖像,在成像清晰的附近區(qū)域每隔10 μm采集一幅圖像,共得到90幅圖像。對比分析處理結(jié)果可知:
(1)絕對方差函數(shù)與梯度向量模方函數(shù)的曲線平滑性差,波動劇烈,存在多個極值點(diǎn),容易誤調(diào)焦,穩(wěn)定性較差,應(yīng)舍棄。
(2)均方差函數(shù)及灰度變化率和函數(shù)具有較大的自動調(diào)焦范圍,計(jì)算速度適中,近似線性變化,但是靈敏度低,適用于大范圍快速粗調(diào)焦,其中灰度變化率和函數(shù)的穩(wěn)定性要優(yōu)于均方差函數(shù)。
(3)Robert梯度函數(shù)、Brenner函數(shù)與梯度向量平方函數(shù)的中等調(diào)焦范圍內(nèi)靈敏度適中,在焦點(diǎn)附近微小區(qū)域內(nèi)靈敏度較高,穩(wěn)定性好,適用于中等范圍內(nèi)的自動調(diào)焦。
(4)拉普拉斯函數(shù)與Tenengrad函數(shù)靈敏度較高,穩(wěn)定性較好,但需要進(jìn)行大量的平方開方運(yùn)算,計(jì)算速度慢,存在偏差,適合用于小范圍精確調(diào)焦[4]。
2 復(fù)合式自動調(diào)焦算法
2.1 復(fù)合式調(diào)焦評價函數(shù)的選擇
灰度變化率和函數(shù)理論基礎(chǔ)是:圖像在離焦時會模糊不清,各像素之間的灰度值變化平緩;當(dāng)越接近正焦平面時,各像素之間的灰度值急劇變化[5-6]。首先選取基準(zhǔn)灰度值g(x0,y0),則其余像素g(x,y)與基準(zhǔn)灰度值 g(x0,y0)的相對變化率為:
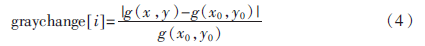
灰度變化率和函數(shù)為:
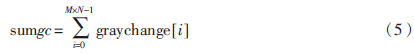
精確調(diào)焦選用梯度向量平方函數(shù),其數(shù)學(xué)表達(dá)式為:
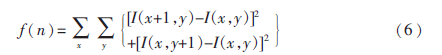
2.2 復(fù)合式自動調(diào)焦策略設(shè)計(jì)
2.2.1 正交平面粗調(diào)焦
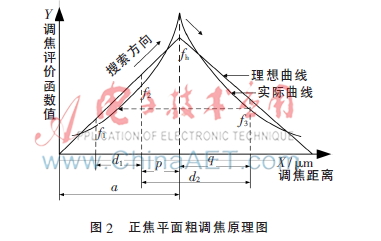
調(diào)焦評價函數(shù)的靈敏度與調(diào)焦區(qū)域大小呈線性關(guān)系,增大調(diào)焦評價區(qū)域有助于提高自動調(diào)焦的精度。大范圍內(nèi)快速粗調(diào)焦選用灰度變化率和函數(shù),它的函數(shù)曲線關(guān)于正焦平面對稱,可用分段線性插值求得一等腰三角形近似代替求解[7]。等腰三角形的高為fh,底邊長約為2a[6]。如圖2所示,正焦平面兩側(cè)有3幀圖像,其調(diào)焦評價函數(shù)值分別為f1、f2、f3,幀間與光軸的分別相距d1、d2,且第2、3幀圖像與正焦平面分別相距p、q,根據(jù)幾何三角形相似有:

由式(7)可解得:
![ZNR@G]GRKCZWWRDWE35L(1R.png ZNR@G]GRKCZWWRDWE35L(1R.png](http://files.chinaaet.com/images/2016/02/22/6359174922876700008456229.png)
在實(shí)際應(yīng)用中,當(dāng)算法開始時在同一方向以1/2景深采集3幀圖像,其對應(yīng)的函數(shù)值分別為K1、K2、K3。若K1<K2<K3,說明此時處于爬坡階段;若K1>K2且K2<K3或K1<K2且K2>K3,說明此時遇到局部噪聲,仍處于爬坡階段;而后選用3倍景深為步長進(jìn)行快速調(diào)焦搜索,當(dāng)相鄰兩點(diǎn)函數(shù)值差值為負(fù)值時停止,通過式(8)計(jì)算得到p或q的值,從而快速把CCD鏡頭移動到正焦平面粗略位置[8]。
2.2.2 正交平面精確調(diào)焦
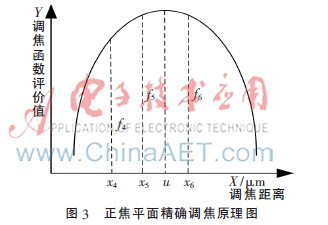
在確定正焦平面粗略位置后,在峰值點(diǎn)附近微小區(qū)域選取梯度向量平方函數(shù)再次調(diào)焦以提高正焦平面的調(diào)焦精度,其函數(shù)曲線形狀與二次曲線相似,如圖3所示。
二次插值函數(shù)的一般數(shù)學(xué)表達(dá)式為:
L(x)=l0(x)y0+l1(x)y1+l2(x)y2(9)
在正焦平面粗略位置采集一幀圖像,其調(diào)焦距離為x4,調(diào)焦函數(shù)值為f4;在正焦平面粗略位置兩側(cè)1/2景深再分別采集一幀圖像,其調(diào)焦距離為x5、x6,調(diào)焦函數(shù)值為f5、f6,則該二次插值曲線表達(dá)式為:
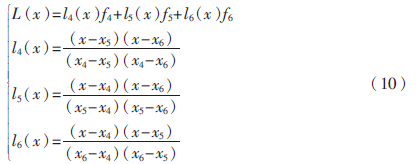
欲求正焦平面的精確位置即是求二次插值曲線的極值點(diǎn)u,需對式(10)求導(dǎo)數(shù)并令其等于0即可,極值點(diǎn)u的計(jì)算公式為:
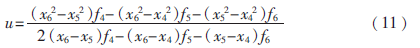
根求取的u值是調(diào)焦初始位置到正焦平面精確位置的距離,需將CCD鏡頭從粗略位置移動(u-p)m實(shí)現(xiàn)鏡頭可精確對焦。若有更高的調(diào)焦精度要求,可多次重復(fù)此過程并求取u的平均值,以減小隨機(jī)誤差。
3 探究實(shí)驗(yàn)與結(jié)果分析
在視覺坐標(biāo)測量儀上對復(fù)合式自動調(diào)焦算法的特性參數(shù)進(jìn)行實(shí)驗(yàn)。相機(jī)采用日本Sony公司的F717系列,采集574×764的圖像,鏡頭采用日本Computar公司的M3Z1228C-MP工業(yè)鏡頭,采用投射式0.68 μm LED紅色光源照明,采用柯拉照明方式以獲取亮度均勻的良好視場。
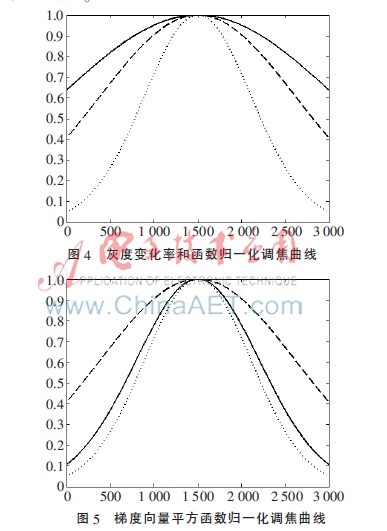
在實(shí)驗(yàn)中分別對線紋尺、精細(xì)掩膜和條形碼進(jìn)行了算法性能測試。實(shí)驗(yàn)過程:首先,移動鏡頭至遠(yuǎn)離正焦平面的位置,得到熵極值的尺寸為256×256的子圖像,在此圖像6 mm范圍內(nèi)利用Visual Basic語言自主研發(fā)的軟件控制鏡頭沿坐標(biāo)測量儀緩慢、平穩(wěn)移動,分別測得灰度變化率和函數(shù)與梯度向量平方函數(shù)歸一化調(diào)焦曲線,分別如圖4、圖5所示。從圖中可以看出,灰度變化率和函數(shù)圖像的半寬度過大,調(diào)焦精度有限,梯度向量平方函數(shù)的調(diào)焦范圍不大,僅能實(shí)現(xiàn)1 500 μm左右范圍的自動調(diào)焦。
選中灰度率和函數(shù)調(diào)焦范圍內(nèi)一點(diǎn)為調(diào)焦起點(diǎn),以3倍景深為初始步長,使用復(fù)合式自動調(diào)焦算法進(jìn)行實(shí)驗(yàn)。當(dāng)進(jìn)行大范圍快速粗略調(diào)焦時將伺服電機(jī)的運(yùn)行速度控制在5 000 pulse/s左右,峰值微小區(qū)域精確調(diào)焦時將伺服電機(jī)的運(yùn)行速度控制在2 000 pulse/s左右,CCD數(shù)碼相機(jī)的曝光時間約為100 ms,灰度變化率和函數(shù)的計(jì)算時間約為1 ms,梯度向量平方函數(shù)的計(jì)算時間約為2 ms,實(shí)驗(yàn)數(shù)據(jù)如表1所示。
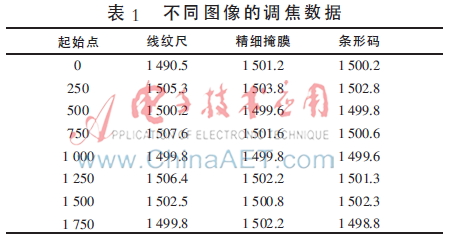
由表1中數(shù)據(jù)計(jì)算可知,復(fù)合式自動調(diào)焦算法的調(diào)焦范圍大,在±1 800 μm范圍內(nèi)調(diào)焦精度可達(dá)10 μm;粗略調(diào)焦時采集16幀圖像即滿足調(diào)焦條件實(shí)現(xiàn)正焦,平均耗時9 s;精確調(diào)焦時采集8幀圖像即滿足調(diào)焦條件實(shí)現(xiàn)正焦,平均耗時5 s。
4 結(jié)論
復(fù)合式自動調(diào)焦算法充分利用了灰度變化率和函數(shù)與梯度向量平方函數(shù)兩種典型自動調(diào)焦算法的優(yōu)點(diǎn)進(jìn)行互補(bǔ),克服了傳統(tǒng)調(diào)焦算法高精度與高效率互斥的矛盾,同時具有調(diào)焦范圍大、通用性強(qiáng)的優(yōu)點(diǎn),能夠完全滿足計(jì)算機(jī)視覺檢測系統(tǒng)要求的使用標(biāo)準(zhǔn),對非接觸型的精密測量的發(fā)展有一定的積極作用。
參考文獻(xiàn)
[1] 王健.基于圖像處理的自動調(diào)焦技術(shù)研究[D].北京:中國科學(xué)院研究生院(光電技術(shù)研究所),2013.
[2] 黃德天.基于圖像技術(shù)的自動調(diào)焦方法研究[D].長春:中國科學(xué)院研究生院(長春光學(xué)精密機(jī)械與物理研究所),2013.
[3] 劉雪超.基于數(shù)字圖像處理的自動調(diào)焦技術(shù)研究[D].長春:中國科學(xué)院研究生院(長春光學(xué)精密機(jī)械與物理研究所),2014.
[4] 胡濤,陳世哲,劉國棟,等.大范圍自動調(diào)焦快速搜索算法[J].光電子·激光,2006(4):464-467.
[5] 莫春紅,劉波,丁璐,等.一種梯度閾值自動調(diào)焦算法[J].紅外與激光工程,2014,43(1):323-327.
[6] 史紅偉,石要武,楊爽.光學(xué)顯微鏡自動調(diào)焦指導(dǎo)函數(shù)的評價與選擇[J].計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報,2013,25(2):235-240.
[7] 楊再華,李玉和,李慶祥,等.一種粗精結(jié)合的圖像反饋?zhàn)詣诱{(diào)焦方法[J].計(jì)算機(jī)工程與設(shè)計(jì),2005,26(9):2271-2273.
[8] 瞿蓬,林喜榮.一種基于圖像處理的自動調(diào)焦系統(tǒng)[J].電子技術(shù)應(yīng)用,2002,28(10):33-35.

