鈕浩東，黃洪瓊

　　（上海海事大學 信息工程學院,上海 201306）

      摘要：針對船舶交通流預測中存在復雜性、非線性、受限因素多等特點，運用果蠅優化算法，建立了優化的廣義回歸神經網絡船舶交通流預測模型。通過利用果蠅優化算法的全局尋優特性對廣義回歸神經網絡進行參數優化，從而實現對船舶交通流的預測。以東海大橋的船舶流量觀測數據為實例對象進行分析，通過MATLAB進行仿真預測，實驗結果表明：FOA-GRNN模型相比于傳統的GRNN模型和BPNN模型具有更高的預測精度和泛化能力，有效地解決了預測過程中數據樣本少、非線性擬合能力差等問題，對水路的規劃、通航管理等方面具有一定的應用價值。

　　關鍵詞：船舶流量；果蠅算法；參數優化；預測；廣義回歸神經網絡

0引言

　　隨著經濟的發展和國際貿易的不斷增長，海上船舶數量顯著增加，中國沿海地區和長江流域的船舶交通量也日益多元化。因此，精準地預測相關水域的船舶交通流量也日趨重要，其不僅能為航道的規劃、設計、管理提供有力依據，還能提高通航效率，降低海上交通事故發生率。影響船舶交通流量預測的因素有很多，涉及政治、經濟、人為等多方面的因素。目前國內外學者提出的預測方法有支持向量機［1］、組合預測［2］、回歸分析［3］等，然而這些單一的預測方法難以滿足在預測精度方面的預期要求。

　　為了克服傳統預測方法存在的預測精度不高、非線性擬合能力不強、計算復雜等方面的不足，本文建立了一種新的船舶流量預測模型，即FO-GRNN模型，首次把果蠅算法（FOA）優化的廣義回歸神經網絡（GRNN）運用到船舶交通流量預測中來。果蠅算法是根據果蠅尋找食物的活動演變而來的新興算法，具有良好的全局尋優能力；另外廣義回歸神經網絡的特點是具備優秀的局部逼近能力、較快的訓練速度、處理非線性問題的優勢明顯。因此將兩者有效地結合起來，通過利用FOA優化GRNN的相關參數來構建最優的預測模型，實現了預測船舶交通流量的目的。

1廣義回歸神經網絡

　　斯坦福大學博士唐納德·施佩希特于20世紀90年代初提出廣義回歸神經網絡模型，其屬于徑向基(RBF)神經網絡的一部分，相比于RBF網絡，GRNN具有較強的局部逼近能力以及較快的學習速度［4］。另外，在樣本數據較少的情況下，廣義回歸神經網絡的預測結果也較優，其網絡結構如圖1所示。此網絡由3個部分組成，分別為輸入層、徑向基層以及線性網絡層。　　

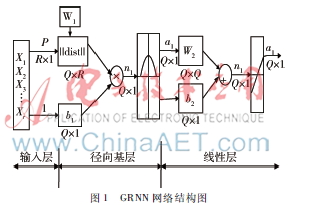
　　網絡的第一層為信號輸入層，輸入向量經輸入層傳送至隱含層，其中隱含層包含Q個神經元，傳遞函數一般用高斯函數R=exp-x-c2σ2表示，式中σ稱為平滑因子。輸出層是一個特定的線性層，該層包含與隱含層數目相同的神經元，并且使用歸一化點積權函數作為該層的權值函數，利用線性函數a2=purelin(n2)表示輸出層的節點函數，從而計算出網絡的輸出值。

2FOA-GRNN預測模型的構建

　　果蠅優化算法是根據果蠅尋找食物的活動演變而來的一種全局尋優的新興算法，在操作性、實用性和收斂速度等方面具有明顯優勢。

　　因為GRNN的性能受到σ取值的影響，所以本文使用果蠅算法來優化Spread值，主要思想就是通過果蠅嗅覺搜尋食物及視覺發現群體所在位置，從而使得Spread值取到最優解，然后使用迭代尋優的方法，將GRNN網絡的預測值與真實值的均方差降至最低，記錄這一時刻的味道濃度值，此值即為σ的最優解。圖2為FOA-GRNN模型的流程圖［5］，學習步驟如下。

　　（1）參數初始化，如果蠅的種群規模、迭代次數和初始位置。

　　（2）隨機規定單個果蠅發現食物的所在位置和間隔距離。

　　（3）因為不清楚食物的具體位置，所以必須先求出所有果蠅相距原點的長度，然后求出味道濃度判定值S。

　　（4）建立味道濃度判定函數，把計算得到的S值代入到函數中，從而得到果蠅所在方位的味道濃度值。濃度判定函數選取GRNN模型里的均方差表示。

　　（5）求解果蠅群體中味道濃度的極值，即求均方差的極小值。

　　（6）記錄最優味道濃度值和此時相應的果蠅位置。

　　（7）開始迭代尋優，循環執行步驟(2)~(5)，假如味道濃度優于前一代，則進行步驟(6)。

　　（8）判斷迭代次數條件是否滿足，若滿足則得到Spread最優解，并將其帶入最優的GRNN模型進行仿真預測，否則返回步驟(2)繼續執行。

3實例仿真與分析

　　3.1實驗數據及參數設置

　　以上海洋山港東海大橋觀測面經過的船舶為研究對象，根據上海洋山港統計的數據，選取2015年4月15日至2015年7月5日的船舶流量數據作為預測的原始數據。前50天數據作為訓練數據，后32天數據作為測試數據。選取上海GDP指數、運輸成本、業務量指數、船舶平均噸位、天氣情況5個指標作為主要影響因素來建立預測模型。為了減小預測誤差，實現多類別樣本的統一分析，確保數據保持在同一數量上，故在實驗前先對數據進行歸一化處理，公式如下所示［6］：

　　仿真試驗時，選取MATLAB神經網絡工具箱中的newgrnn函數來得到Spread最優值，構建最佳的FOA-GRNN船舶流量預測模型。通過反復驗算設定FOA的參數如下：初始化果蠅群體位置區間為［0,100］，果蠅群體規模為30，迭代次數為200。經過FOA優化后，得到最優的Spread值為0.002 2。

　　3.2仿真結果對比分析

　　為了對實驗結果進行對比分析，本文分別計算了3種算法的MAD、MAPE、RMS。設xt為實際流量值，t為預測值，n為預測序列總數，其相應公式依次為［7］：

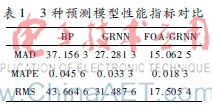
　　將這3種預測模型進行性能指標對照，其比較結果如表1所示。此外，為了凸顯本文優化方法的優越性，分別對BP神經網絡模型、GRNN模型和FOAGRNN模型進行表13種預測模型性能指標對比BPGRNNFOAGRNNMAD37.156 327.281 315.062 5MAPE0.045 60.033 30.018 3RMS43.664 631.487 617.505 4仿真實驗及比較，仿真結果如圖3~圖5所示。

　　由圖3~圖5及表1可知，雖然BP網絡模型和單一的GRNN網絡模型都得到了相應的預測結果，但是在預測精度上還是不及FOAGRNN模型。由于BP神經網絡需要大量的訓練樣本，有時樣本數條件無法達到要求，此外由于神經網絡中的過擬合現象和GRNN中Spread值的選擇問題，使得這兩種算法的預測精度沒有達到預期的要求。FOA具有較強的全局尋優能力，利用FOA優化GRNN模型的Spread值，得到其最優解，使得預測誤差達到最小。

　　由表1可知，應用FOAGRNN模型預測的MAD、MAPE、RMS值都比單一的GRNN模型和BP模型小，由此說明，相對于BP和GRNN網絡，FOAGRNN網絡模型的預測誤差較小并且具有較高的穩定性，FOAGRNN模型在預測能力、逼近能力等方面皆具有較強的優勢。

4結論

　　本文首次將果蠅算法優化的廣義回歸神經網絡模型應用于船舶交通流量預測中，根據FOA算法的全局尋優特性對GRNN網絡中的Spread值進行優化，充分考慮多方面因素的影響，構建了FOAGRNN船舶交通流量預測模型，其具有如下特點：

　　（1）良好的擬合能力和泛化能力。通過MATLAB仿真實驗證明此模型具有良好的預測能力，與BP和GRNN模型相比，該模型的絕對值平均誤差、相對誤差絕對值平均值、均方根誤差都比較小，具備更優的預測精度。

　　（2）良好的穩定性和快速收斂能力。該模型需要確定的參數少，能夠很好地避免人為主觀臆斷的影響。

　　綜合分析，FOAGRNN模型的實現過程簡單，泛化能力強，預測精度較高，為船舶交通流量預測提供了一種新途徑。

參考文獻

　　［1］ 馮宏祥，肖英杰.基于支持向量機的船舶交通流量預測模型［J］.中國航海，2011,34(4)：6266.

　　［2］ 呂靖，方祥麟.船舶交通量的組合預測模型與方法［J］.大連海事大學學報，1996，22(2)： 3335.

　　［3］ 張杏谷.回歸分析方法在VTS預測研究中的應用［J］.中國航海，1996(2)：3235.

　　［4］ 劉敬賢，劉振東.基于廣義回歸神經網絡的船舶交通量預測模型［J］.中國航海，2011，34(2)：7478.

　　［5］ 聶娜娜.修正型果蠅算法優化GRNN網絡的尾礦庫安全預測［J］.計算機工程，2015，41(4)： 267272.

　　［6］ 沈浩,黃洪瓊.基于PSO優化SVM的船舶流量預測算法［J］.微型機與應用,2015,34(5):7375.

　　［7］ 郎茂祥.預測理論與方法［M］.北京：清華大學出版社，北京交通大學出版社，2011.